
1. 函数 是减函数的区间为
( )
是减函数的区间为
( )
A.  B.
B.  C.
C.
 D.
D. 
13. 解:  ,
,  或
或
又 成等差数列,
成等差数列, …………①
…………①
当 时,
时,  代入①
代入①
 (成立),
(成立), 
当 时, 不成立.
时, 不成立.
12. 解: 证(1)由
知
又 ,
,
则 ∴
∴

故数列 是首项为1, 公比为2的等比数列.
是首项为1, 公比为2的等比数列.
证(2) 由(I)知,  , 于是
, 于是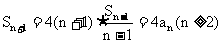
又 ,则
,则 , 因此对于任意正整数
, 因此对于任意正整数 都有
都有 .
.
11. 解: 
 (舍去),
(舍去), 
7.  ,
,  8. 510
; 9. 1
; 10.
117 .
8. 510
; 9. 1
; 10.
117 .
(二) 专题测试与练习
(一) 典型例题
例1 
例2 



例3 (1) 由题设


(2) 若
当 故
故
若
当
故对于
11. 已知等差数列 中,
中, 
 求a1和k.
求a1和k.
12. 数列 的前n项和记为
的前n项和记为 , 已知
, 已知 ,
,


证明: (1)数列 是等比数列;(2)
是等比数列;(2) 
13. 等比数列同时满足下列三个条件:
(1)
 (2)
(2)  (3)三个数
(3)三个数 成等差数列. 试求数列
成等差数列. 试求数列
 的通项公式.
的通项公式.
数列的基本性质解答
10. 已知等差数列 ,
,  .
.
9. 等比数列 中,
中,  则a 4 =
.
则a 4 =
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com