
6.本题等价于求函数x=f(y)=(y+3)·|y-1|+(y+3)在 时的最小值.易得
时的最小值.易得
5. 若d=0或q=1,则am=bm.
若d≠0,画出an=a1+(n-1)d与bn=b1·qn-1的图象,
易知am>bm,故am≥bm.
6.设集合M={(x,y)|x=(y+3)|y-1|+(y+3),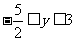 },若(a,b)∈M,且对M中的其它元素(c,d),总有c≥a,则a的值是______________.
},若(a,b)∈M,且对M中的其它元素(c,d),总有c≥a,则a的值是______________.
◆简答:1-4.BABC; 4.设左、右臂长分别是 则
则 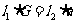 ,
,
①×②得G2= , ∴G=
, ∴G= ,由于
,由于 ,故
,故
 >
> 
5.在等差数列{an}与等比数列{bn}中,a1=b1>0,an=bn>0,若m<n,则am与bm的大小关系是____________.
4.今有一台坏天平,两臂长不等,其余均精确,有人要用它称物体的重量,他将物体放在左右托盘各称一次,取两次称量结果分别为a,b.设物体的真实重量为G,则 ( )
A. =G
B.
=G
B.  ≤G
C.
≤G
C.  >G
D.
>G
D. <G
<G
3.某工厂年产值第二年比第一年增长百分率为p1,第三年比第二年增长的百分率为p2,第四年比第三年增长的百分率为p3,若p1+p2+p3=m,m为常数,则年平均增长率p的最大值为( )
A. B.
B. C.
C. D.
D.

2.(2004湖南)设集合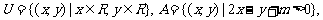
 ,那么点P(2,3)
,那么点P(2,3) 的充要条件是( )
的充要条件是( )
A.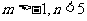 B.
B.
C. D.
D.
1.(2004湖北)函数 上的最大值和最小值之和为a,则a的值为
( )
上的最大值和最小值之和为a,则a的值为
( )
A. B.
B. C.2 D.4
C.2 D.4
4.利用不等式解应用题的基本步骤:
(1)审题,(2)建模(不等式或函数),(3)求解,(4)作答
3.不等式的应用范围十分广泛,许多问题,最终都可归结为不等式的求解、证明或求最值。这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建立函数式求最大值或最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com