六，后记

2．掌握两个公式：

1．根式的概念：若n＞1且，则

为偶数时，；

3、求值化简：　 ；　 ；　 ；　 ()

2、 化简：　 ；

1. 计算或化简：； (推广：， a0).

3、例题讲解

(P_5O例题1)：求下列各式的值

2. 教学根式的概念及运算：

① 复习实例蕴含的概念：,就叫4的平方根；，3就叫27的立方根.

探究：,就叫做的？次方根, 依此类推,若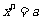,那么叫做的次方根.

② 定义n次方根：一般地，若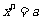,那么叫做的次方根.( 　th　 root ),其中,

简记：.　　 例如：，则

③ 讨论：当n为奇数时, n次方根情况如何？, 例如: ,,　

记：

当n为偶数时，正数的n次方根情况？ 例如: ,的4次方根就是, 记：

强调：负数没有偶次方根,0的任何次方根都是0, 即.

④ 练习：,则的4次方根为　　 ； , 则的3次方根为　　　 .

⑤ 定义根式：像的式子就叫做根式(radical), 这里n叫做根指数(radical exponent),　 a叫做被开方数(radicand).

⑥ 计算、、 → 探究： 、的意义及结果？ (特殊到一般)

结论：. 当是奇数时，；当是偶数时，

1. 教学指数函数模型应用背景：

①　　 探究下面实例，了解指数指数概念提出的背景，体会引入指数函数的必要性.

实例1.某市人口平均年增长率为1.25℅，1990年人口数为a万，则x年后人口数为多少万？

实例2. 给一张报纸，先实验最多可折多少次(8次)

计算：若报纸长50cm，宽34cm，厚0.01mm，进行对折x次后，问对折后的面积与厚度？

② 书P52 问题1. 国务院发展研究中心在2000年分析，我国未来20年GDP(国内生产总值)年平均增长率达7.3℅， 则x年后GDP为2000年的多少倍？

　 书P52 问题2. 生物死亡后，体内碳14每过5730年衰减一半(半衰期)，则死亡t年后体内碳14的含量P与死亡时碳14的关系为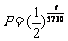. 探究该式意义？

③小结：实践中存在着许多指数函数的应用模型，如人口问题、银行存款、生物变化、自然科学.

2、回顾初中根式的概念：如果一个数的平方等于a，那么这个数叫做a的平方根；如果一个数的立方等于a，那么这个数叫做a的立方根.　 → 记法：