
12. 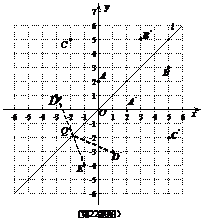 解:(1)如图:
解:(1)如图: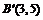 ,
,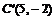 ;(2) (b,a) ;
;(2) (b,a) ;
(3)由(2)得,D(1,-3) 关于直线l的对称点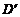 的坐标为(-3,1),连接
的坐标为(-3,1),连接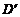 E交直线l于点Q,此时点Q到D、E两点的距离之和最小
E交直线l于点Q,此时点Q到D、E两点的距离之和最小
设过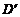 (-3,1) 、E(-1,-4)的设直线的解析式为
(-3,1) 、E(-1,-4)的设直线的解析式为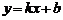 ,则
,则
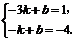 ,∴
,∴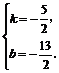 ,∴
,∴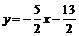 .由
.由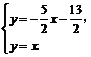 得
得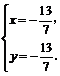 ,∴所求Q点的坐标为(
,∴所求Q点的坐标为(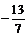 ,
,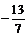 )
)
11. 解:由图象可知,点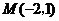 在直线
在直线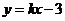 上,
上,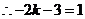 .解得
.解得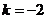 .
.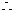 直线的解析式为
直线的解析式为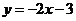 .令
.令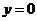 ,可得
,可得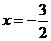 .
.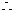 直线与
直线与 轴的交点坐标为
轴的交点坐标为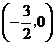 .令
.令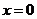 ,可得
,可得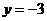 .
.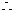 直线与
直线与 轴的交点坐标为
轴的交点坐标为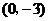 .
.
10. 解:(1)由直角三角形纸板的两直角边的长为1和2,
知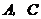 两点的坐标分别为
两点的坐标分别为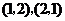 .
.
设直线 所对应的函数关系式为
所对应的函数关系式为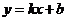 .···························································· 2分
.···························································· 2分
有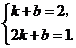 解得
解得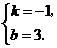
 所以,直线
所以,直线 所对应的函数关系式为
所对应的函数关系式为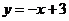 .····················································· 4分
.····················································· 4分
(2)①点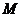 到
到 轴距离
轴距离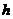 与线段
与线段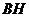 的长总相等.
的长总相等.
因为点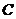 的坐标为
的坐标为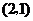 ,
,
所以,直线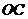 所对应的函数关系式为
所对应的函数关系式为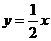 .
.
又因为点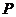 在直线
在直线 上,
上,
所以可设点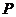 的坐标为
的坐标为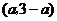 .
.
过点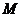 作
作 轴的垂线,设垂足为点
轴的垂线,设垂足为点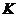 ,则有
,则有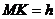 .
.
因为点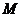 在直线
在直线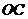 上,所以有
上,所以有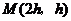 .······················· 6分
.······················· 6分
因为纸板为平行移动,故有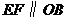 ,即
,即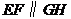 .
.
又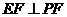 ,所以
,所以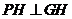 .
.
法一:故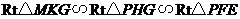 ,
,
从而有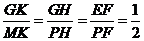 .
.
得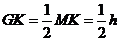 ,
,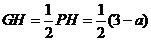 .
.
所以 .
.
又有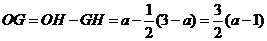 .························································ 8分
.························································ 8分
所以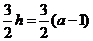 ,得
,得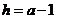 ,而
,而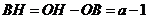 ,
,
从而总有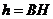 .····································································································· 10分
.····································································································· 10分
法二:故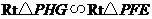 ,可得
,可得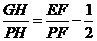 .
.
故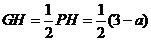 .
.
所以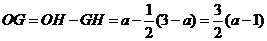 .
.
故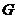 点坐标为
点坐标为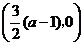 .
.
设直线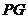 所对应的函数关系式为
所对应的函数关系式为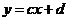 ,
,
则有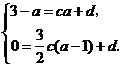 解得
解得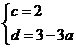
所以,直线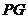 所对的函数关系式为
所对的函数关系式为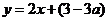 .·············································· 8分
.·············································· 8分
将点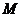 的坐标代入,可得
的坐标代入,可得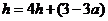 .解得
.解得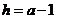 .
.
而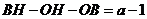 ,从而总有
,从而总有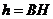 .························································· 10分
.························································· 10分
②由①知,点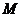 的坐标为
的坐标为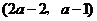 ,点
,点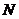 的坐标为
的坐标为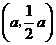 .
.
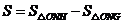
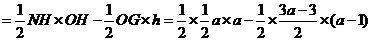
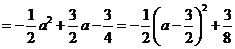 .····································································· 12分
.····································································· 12分
当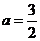 时,
时,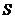 有最大值,最大值为
有最大值,最大值为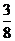 .
.
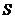 取最大值时点
取最大值时点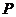 的坐标为
的坐标为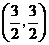 . 14分
. 14分
9.
解:(1)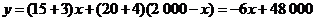 ······························· (3分)
······························· (3分)
(2)由题意,可得: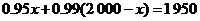 .
.
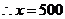 .·········································································································· (5分)
.·········································································································· (5分)
当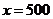 时,
时,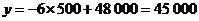 .
.
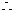 造这片林的总费用需45 000元.········································································· (8分)
造这片林的总费用需45 000元.········································································· (8分)
8.
解:(1)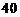 ;
;
(2)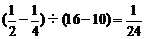 ,
,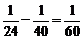
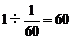 (天)
(天)
答:乙队单独完成这项工程要60天.
(3)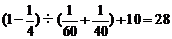 (天)
(天)
答:图中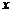 的值是28.
的值是28.
7. 解:(1)设 与
与 之间的关系为一次函数,其函数表达式为
之间的关系为一次函数,其函数表达式为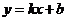 ··················· 1分
··················· 1分
将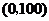 ,
,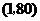 代入上式得,
代入上式得,
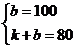 解得
解得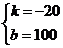
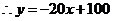 ········································································································· 4分
········································································································· 4分
验证:当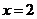 时,
时,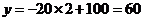 ,符合一次函数;
,符合一次函数;
当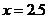 时,
时,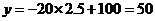 ,也符合一次函数.
,也符合一次函数.
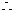 可用一次函数
可用一次函数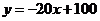 表示其变化规律,
表示其变化规律,
而不用反比例函数、二次函数表示其变化规律.···························································· 5分
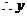 与
与 之间的关系是一次函数,其函数表达式为
之间的关系是一次函数,其函数表达式为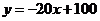 ································ 6分
································ 6分
(2)当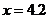 时,由
时,由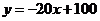 可得
可得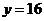
即货车行驶到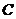 处时油箱内余油16升.········································································ 8分
处时油箱内余油16升.········································································ 8分
(3)方法不唯一,如:
方法一:由(1)得,货车行驶中每小时耗油20升,····················································· 9分
设在 处至少加油
处至少加油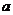 升,货车才能到达
升,货车才能到达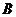 地.
地.
依题意得,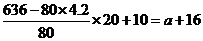 ,···························································· 11分
,···························································· 11分
解得,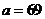 (升)··································································································· 12分
(升)··································································································· 12分
方法二:由(1)得,货车行驶中每小时耗油20升,····················································· 9分
汽车行驶18千米的耗油量: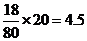 (升)
(升)
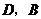 之间路程为:
之间路程为: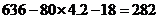 (千米)
(千米)
汽车行驶282千米的耗油量:
 (升)······························································································· 11分
(升)······························································································· 11分
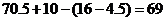 (升)················································································ 12分
(升)················································································ 12分
方法三:由(1)得,货车行驶中每小时耗油20升,····················································· 9分
设在 处加油
处加油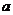 升,货车才能到达
升,货车才能到达 地.
地.
依题意得,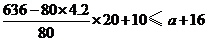 ,
,
解得,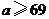 ············································································································· 11分
············································································································· 11分
 在
在 处至少加油
处至少加油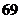 升,货车才能到达
升,货车才能到达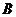 地.·························································· 12分
地.·························································· 12分
6. 解:(1)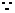 特征数为
特征数为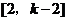 的一次函数为
的一次函数为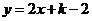 ,
,
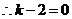 ,
,
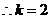 .
.
(2)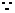 抛物线与
抛物线与 轴的交点为
轴的交点为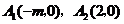 ,
,
与 轴的交点为
轴的交点为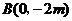 .
.
若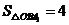 ,则
,则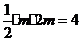 ,
,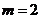 ;
;
若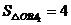 ,则
,则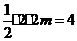 ,
,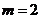 .
.
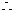 当
当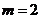 时,满足题设条件.
时,满足题设条件.
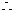 此时抛物线为
此时抛物线为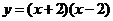 .
.
它与 轴的交点为
轴的交点为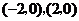 ,
,
与 轴的交点为
轴的交点为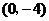 ,
,
 一次函数为
一次函数为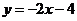 或
或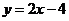 ,
,
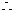 特征数为
特征数为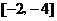 或
或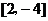 .
.
5. 解⑴y=(63-55)x+(40-35)(500-x)……………3分
=2x+2500。即y=2x+2500(0≤x≤500),………………4分
⑵由题意,得55x+35(500-x)≤20000,………………6分
解这个不等式,得x≤125,………………………………7分
∴当x=125时,y最大值=3×12+2500=2875(元),…………9分
∴该商场购进A、B两种品牌的饮料分别为125箱、375箱时,能获得最大利润2875元.………………………………………………………………10分
4. 解:设这个一次函数的解析式为y=kx+b.
则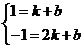 解得
解得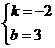 ,函数的解析式为y=-2x+3.
,函数的解析式为y=-2x+3.
由题意,得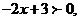 得
得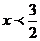 ,所以使函数为正值的x的范围为
,所以使函数为正值的x的范围为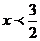
3. 解:(1)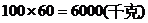 ,所以不能在60天内售完这些椪柑,
,所以不能在60天内售完这些椪柑,
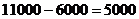 (千克)
(千克)
即60天后还有库存5000千克,总毛利润为
W=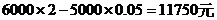 ;
;
(2)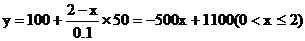
要在2月份售完这些椪柑,售价x必须满足不等式
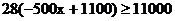
解得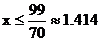
所以要在2月份售完这些椪柑,销售价最高可定为1.4元/千克。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com