
3. (2004湖南)设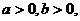 则以下不等式中不恒成立的是 (
)
则以下不等式中不恒成立的是 (
)
A.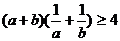 B.
B.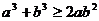
C.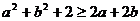 D.
D.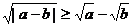
2.下列结论正确的是 ( )
A.当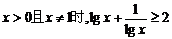 B.
B.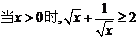
C.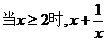 的最小值为2 D.当
的最小值为2 D.当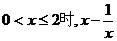 无最大值
无最大值
1.(2006安徽)设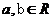 ,已知命题
,已知命题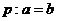 ;命题
;命题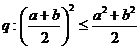 ,则
,则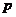 是
是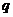 成立的( )
成立的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
3.在用均值定理解决实际问题时,要理解题意,设变量时要把要求最大值或最小值的变量定为函数,建立相应的函数关系式,在定义域内,求出函数的最大值或最小值.
同步练习 6.2算术平均数 几何平均数
[选择题]
2.掌握公式形式特征,能正用、逆用和变形运用,会 “添拆项”凑定值和等号成立的条件。
1.掌握均值不等式,正确理解它的运用条件和“取最值”的条件;
3.在运用均值不等式求最值时,必须保证“一正,二定,三等”.凑出定值是关键!“=”成立必须保证,若有几步放缩,只要每步取等号的条件相同即可.
[例2]已知ab+a+2b=30,(a>0,b>0),求证:ab≤18.
证明:法1:由已知,(a+2)(b+1)=32,
ab=30-(a+2b)=34-[(a+2)+2(b+1)]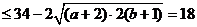
法2:由已知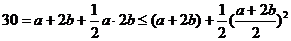
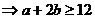 ,∴ab=30-(a+2b)≤18
,∴ab=30-(a+2b)≤18
法3:由已知得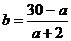
∴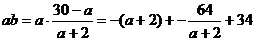
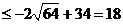
[例3]已知:a>b>c>d,求证: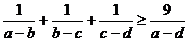 .
.
证明: ∵a-d=(a-b)+(b-c)+(c-d),题中出现了“和”与“倒数和”
∴利用调和平均数与算术平均数的关系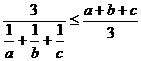
得: 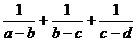
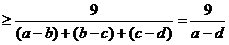
[例4] (2005北京)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量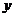 (千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为:
(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为: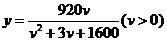 .
.
(1)在该时段内,当汽车的平均速度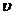 为多少时,车流量最大?最大车流量为多少?(精确到
为多少时,车流量最大?最大车流量为多少?(精确到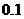 千辆/小时)
千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
解:(Ⅰ)依题意,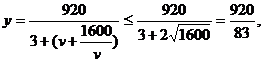
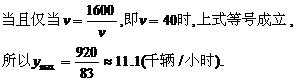
(Ⅱ)由条件得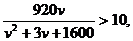
整理得v2-89v+1600<0,
即(v-25)(v-64)<0,解得25<v<64.
答:当v=40千米/小时,车流量最大,最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25千米/小时且小于64千米/小时.
[研讨.欣赏]在△ABC中,∠C=90°,AC+BC=l(定值),将图形沿AB的中垂线折叠,使点A落在点B上,
求图形未被遮盖部分面积的最大值.
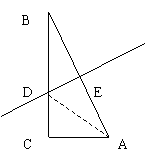
解:将图形沿AB的中垂线折叠,使点A落在点B上,
未被遮盖部分是Rt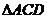
设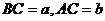 ,
,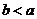 ,则
,则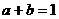 ,
,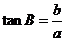
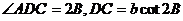
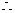 Rt
Rt  的面积
的面积
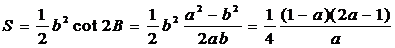
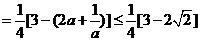
当且仅当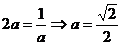 时,
时,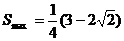
故图形未被遮盖部分面积的最大值是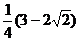 .
.
[例1](1)已知a,b为正常数,x,y为正实数,且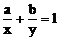 ,求x+y的最小值。
,求x+y的最小值。
(2)若a>b>0, 求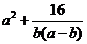 的最小值
的最小值
(3)求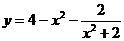 的最大值
的最大值
解(1)法一:直接利用基本不等式: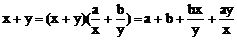 ≥
≥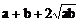 当且仅当
当且仅当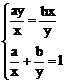 ,即
,即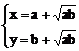 时等号成立
时等号成立
说明:为了利用均值不等式,本题利用了“1”的逆代换。
法二:消元化为一元函数
由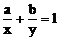 得
得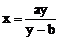
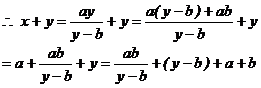
∵ x>0,y>0,a>0 ∴ 由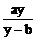 >0得y-b>0
>0得y-b>0
∴ x+y≥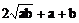
当且仅当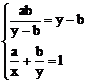 ,即
,即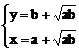 时,等号成立
时,等号成立
法三:三角代换.令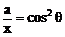 ,
,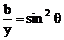 ,
,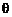 ∈(0,
∈(0,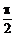 )
)
∴ 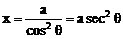 ,
,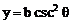
∴ x+y=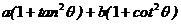
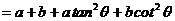 ≥
≥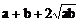
当且仅当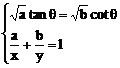 时,等号成立
时,等号成立
(2)分析: 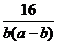 的分母(a-b)b,而(a-b)+b=a, 故问题突破口已显然! 也可以逐步进行:先对b求最小值
的分母(a-b)b,而(a-b)+b=a, 故问题突破口已显然! 也可以逐步进行:先对b求最小值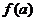 ,然后在对a求最小值
,然后在对a求最小值
解法一: 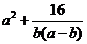 =[(a-b)+b]2 +
=[(a-b)+b]2 +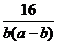
≥[2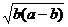 ]2 +
]2 +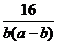 =4(a-b)b+
=4(a-b)b+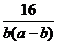 ≥16
≥16
当且仅当b=(a-b)且(a-b)b=2,即a=2b=2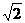 时取等号,故
时取等号,故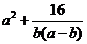 的最小值为16
的最小值为16
解法二: 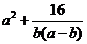
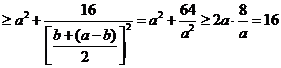
当且仅当b=(a-b)且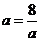 ,
,
即a=2b=2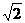 时取等号,故
时取等号,故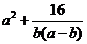 的最小值为16
的最小值为16
(3)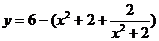
(若由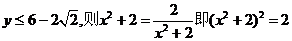 无解“=”不成立)
无解“=”不成立)
令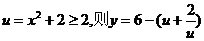 ,可以证明y(u)在
,可以证明y(u)在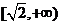 递减
递减
∴u=2,即x=0时,ymax=3
◆ 提炼方法:1.(1)题法一将“1”利用已知回代,充分利用了倒数关系,巧妙灵活;
2.法二,三是常用的两种消元方法,即代数消元和三角换元,要熟练掌握.
5. 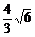 ; 6.
; 6. 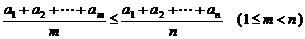
和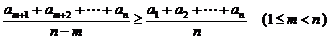
4.令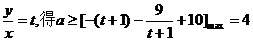
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com