
1、(2002年新课程卷)平面直角坐标系中,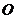 为坐标原点,已知
为坐标原点,已知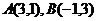 ,若点
,若点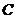 满足
满足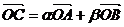 ,其中
,其中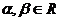 ,且
,且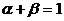 ,则点
,则点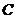 的轨迹方程为( )
的轨迹方程为( )
A. 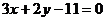 B.
B. 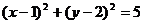
C. 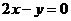 D.
D. 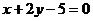
例4、已知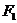 ,F椭圆
,F椭圆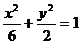 的两个焦点,过点F的直线BC交椭圆于B、C两点,
的两个焦点,过点F的直线BC交椭圆于B、C两点,
(1)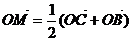 ,求点M的轨迹方程.
,求点M的轨迹方程.
[答案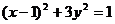 ]
]
(2)若相应于焦点F的准线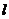 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.设
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.设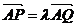 (
(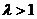 ),过点P且平行于准线
),过点P且平行于准线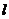 的直线与椭圆相交于另一点M,证明:
的直线与椭圆相交于另一点M,证明: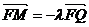 .
.
解:(1)略
(2) 证明: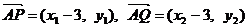 .由已知得方程组
.由已知得方程组
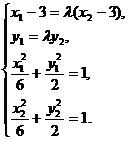
注意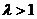 ,解得
,解得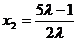
因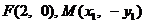 ,故
,故
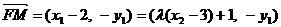
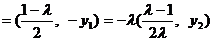 .
.
而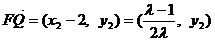 ,所以
,所以
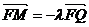 .
.
[结论发散]设P(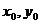 )为椭圆上一点,
)为椭圆上一点,
(1)求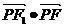 的Min
的Min
(2)求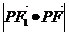 的Max
的Max
(3)当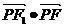 <0时,
<0时,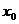 的取值范围。
的取值范围。
(4)若相应于焦点F的准线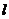 与x轴相交于点A,
与x轴相交于点A,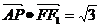 ,求
,求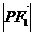
(5)已知点M的坐标为(2,3),求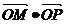 的最值。
的最值。
(6)已知点Q的坐标为(1,1),求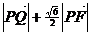 的最小值
的最小值
(7)已知点Q的坐标为(1,1),求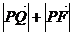 的最值
的最值
[提示] 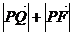
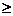
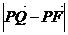 =
=
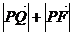 =2a+
=2a+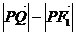
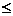 2a+
2a+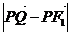 =2a+
=2a+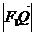
例5.已知A、B为抛物线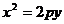 (p>0)上两点,直线AB过焦点F,A、B在准线上的射影分别为C、D,
(p>0)上两点,直线AB过焦点F,A、B在准线上的射影分别为C、D,
(1) 若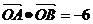 ,求抛物线的方程。
,求抛物线的方程。
(2) CD是否恒存在一点K,使得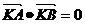
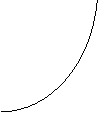
 Y
Y


 A
A

F P
 B
B
 X
X
O

D K C
解:(1)提示:记A(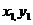 )、B (
)、B (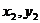 )设直线AB方程为
)设直线AB方程为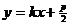 代入抛物线方程得
代入抛物线方程得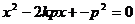
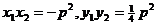
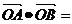
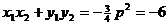
(2)设线段AB中点P在在准线上的射影为T,
则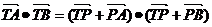
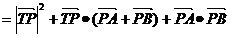
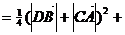
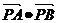 =
=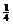
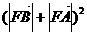 -
-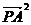 =
=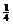
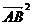 -
-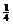
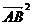 =0
=0
故存在点K即点T,使得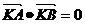
[实质:以AB为直径的圆与准线相切]
[结论发散1] y轴上是否恒存在一点K,使得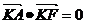
[实质:以AF为直径的圆与y轴相切]
[结论发散2]求证:
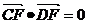
[结论发散3]求证:存在实数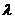 使得
使得 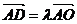
[实质:证明A、O、D三点共线(2001年高考题)]
[结论发散4] 设线段AB中点P在在准线上的射影为T,证明: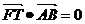
[题设变更1] 已知A、B为抛物线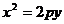 (p>0)上两点,
(p>0)上两点,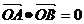 ,点C坐标为
,点C坐标为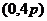
(1) 求证: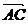 ∥
∥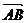
(2)若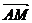 =
=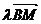 (
(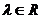 )且
)且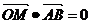 试求点M的轨迹方程。
试求点M的轨迹方程。
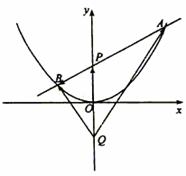
[题设变更2](2004全国湖南文21)如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.设点P分有向线段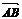 所成的比为
所成的比为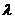 ,证明:
,证明:
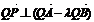 ;
;
解:依题意,可设直线AB的方程为 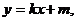 代入抛物线方程
代入抛物线方程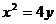 得
得
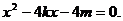 ①
①
设A、B两点的坐标分别是 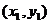 、
、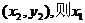 、x2是方程①的两根.
、x2是方程①的两根.
所以 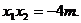
由点P(0,m)分有向线段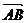 所成的比为
所成的比为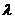 ,
,
得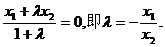
又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而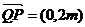 .
.
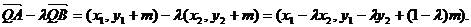
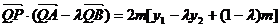
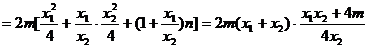
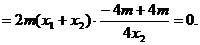
所以 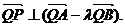
思维能力训练
例1.已知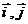 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设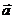 =
=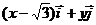 ,
, 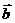 =
=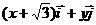 ,且满足|
,且满足|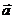 |+|
|+|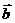 |=4.
|=4.
(1)求点P(x,y)的轨迹C的方程.
(2)如果过点Q(0,m)且方向向量为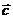 =(1,1) 的直线l与点P的轨迹交于A,B两点,当
=(1,1) 的直线l与点P的轨迹交于A,B两点,当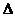 AOB的面积取到最大值时,求m的值。
AOB的面积取到最大值时,求m的值。
解:(1)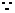
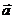 =
=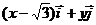 , |
, |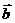 |=
|=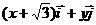 ,且|
,且|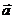 |+|
|+|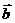 |=4.
|=4.
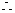 点P(x,y)到点(
点P(x,y)到点(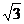 ,0),(-
,0),(-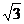 ,0)的距离这和为4,故点P的轨迹方程为
,0)的距离这和为4,故点P的轨迹方程为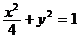
(2)设A(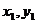 ),B(
),B(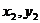 )依题意直线AB的方程为y=x+m.代入椭圆方程,得
)依题意直线AB的方程为y=x+m.代入椭圆方程,得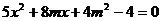 ,则
,则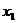 +
+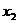 =-
=-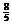 m,
m, 
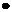
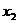 =
=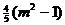
因此,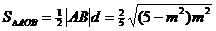
当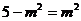 时,即m=
时,即m=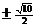 时,
时,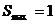
[题设变式I.1] 已知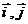 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设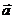 =
=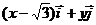 ,
, 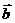 =
=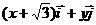 ,且满足||
,且满足||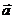 |-|
|-|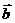 ||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
[题设变式I.2] 已知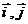 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设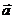 =
=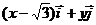 ,
, 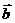 =
=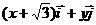 ,且满足
,且满足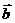
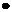
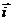 =|
=|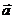 |.求点P(x,y)的轨迹C的方程.
|.求点P(x,y)的轨迹C的方程.
[提示:设K(-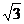 ,0),F (
,0),F (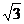 ,0),则
,0),则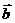
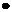
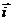 表示
表示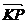 在x轴上射影,即点P到x= -
在x轴上射影,即点P到x= -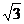 的距离,所以点P到定点F的距离与到定直线x= -
的距离,所以点P到定点F的距离与到定直线x= -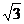 的距离比为1,故点P的轨迹是以(
的距离比为1,故点P的轨迹是以(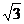 ,0)为焦点以x= -
,0)为焦点以x= -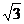 为准线抛物线]
为准线抛物线]
[题设变式I.3] 已知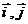 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设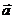 =
=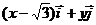 ,
, 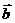 =
=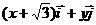 ,且满足
,且满足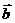
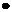
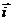 =
=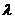 |
|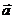 |.求点P(x,y)的轨迹C的方程.
|.求点P(x,y)的轨迹C的方程.
[提示:设K(-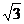 ,0),F (
,0),F (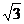 ,0),则
,0),则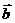
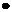
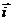 表示
表示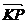 在x轴上射影,即点P到x= -
在x轴上射影,即点P到x= -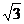 的距离,所以点P到定点F的距离与到定直线x= -
的距离,所以点P到定点F的距离与到定直线x= -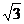 的距离比为
的距离比为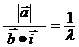 ,当
,当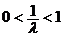 时,点P的轨迹是以(
时,点P的轨迹是以(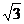 ,0)为焦点,以x= -
,0)为焦点,以x= -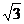 为相应准线的椭圆;当
为相应准线的椭圆;当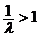 时,点P的轨迹是以(
时,点P的轨迹是以(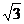 ,0)为焦点,以x= -
,0)为焦点,以x= -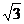 为相应准线的双曲线的右支;若想得到双曲线的双支
为相应准线的双曲线的右支;若想得到双曲线的双支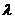 应满足什么条件?]
应满足什么条件?]
[题设变式I.4] 已知平面上两定点K、F,P为一动点,满足,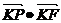
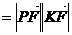 .求点P(x,y)的轨迹C的方程.(以F焦点,过K且垂直于KF的直线为准线的抛物线)
.求点P(x,y)的轨迹C的方程.(以F焦点,过K且垂直于KF的直线为准线的抛物线)
[题设变式I.5] 已知平面上两定点K、F,P为一动点,满足,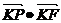
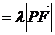 .求点P(x,y)的轨迹C的方程.(以F焦点,过K且垂直于KF的直线为准线的圆锥曲线。)
.求点P(x,y)的轨迹C的方程.(以F焦点,过K且垂直于KF的直线为准线的圆锥曲线。)
[考题] 已知点A(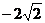 ,0),B(
,0),B(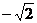 ,0)动点P满足
,0)动点P满足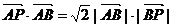
(1)若动点P的轨迹记作曲线C1,求曲线C1的方程.
(2)已知曲线C1交y轴正半轴于点Q,过点D(0,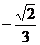 )作斜率为k的直线交曲线
)作斜率为k的直线交曲线
C1于M、N点,求证:无论k如何变化,以MN为直径的圆过点Q.(解答见附页)
[题设变式II.1] 已知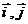 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设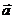 =
=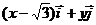 ,
, 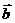 =
=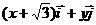 ,且满足|
,且满足|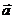 +
+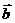 |=4..求点P(x,y)的轨迹C的方程. (
|=4..求点P(x,y)的轨迹C的方程. (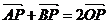 ,点P轨迹为圆,其中A(
,点P轨迹为圆,其中A(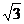 ,0),B(-
,0),B(-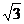 ,0))
,0))
[题设变式II.2] 已知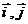 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设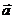 =
=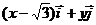 ,
, 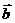 =
=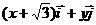 ,且满足
,且满足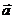
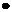
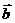 =6.求点P(x,y)的轨迹C的方程. (轨迹为圆)
=6.求点P(x,y)的轨迹C的方程. (轨迹为圆)
例2、已知两点M(-2,0),N(2,0),动点P在y轴上的射影是H,如果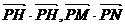 分别是公比q=2的等比数列的第三、第四项.
分别是公比q=2的等比数列的第三、第四项.
(1)求动点P的轨迹C的方程;
(2)已知过点N的直线l交曲线C于x轴下方两个不同的点,A、B,设R为AB的中点,若过点R与定点Q(0,-2)的直线交x轴于点D(x0,0),求x0的取值范围.
导析 (1)设P(x,y),则H(0,y),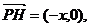
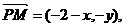
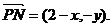
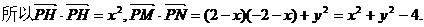
又因为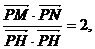 所以有
所以有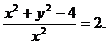
所以点P的轨迹方程为y2-x2=4(x≠0).
(2)设AB:y=k(x-2),A(x1y1),B(x2y2),R(x3y3).
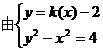 化简得(k2-1)x2-4k2x=4(k2-1)=0.
化简得(k2-1)x2-4k2x=4(k2-1)=0.
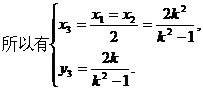 所以
所以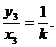
所以DQ的方程为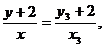 令y=0,得
令y=0,得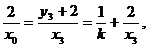
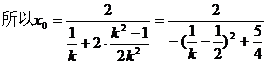 又由
又由
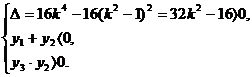 可得k2>
可得k2>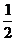 ,由题意可知
,由题意可知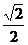 <k<1,
<k<1,
所以1<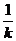 <
<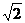 ,所以
,所以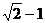 <-(
<-(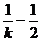 )2+
)2+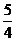 <1, 所以2<x0<2+
<1, 所以2<x0<2+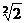 .
.
故所求的x0的取值范围为(2,2+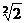 ).
).
[题后反思]若改变q 的值能否构造出椭圆来呢?
[当0<q<1时,点P的轨迹为椭圆]
例3、如图所示,点F (a,0)(a>0),点P在y轴上运动,M在x轴上,N为动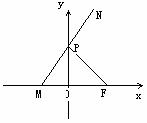 点,且
点,且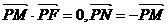
(1)求点N的轨迹C的方程;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点K(-a,0),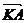 与
与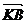 的夹角为
的夹角为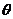 ,求证:0<
,求证:0<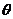 <
<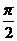 .
.
[答案提示] (1)点N的轨迹C的方程为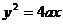
[变化]点F (a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,
且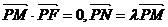 (
(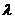 为常数)求点N的轨迹仍为抛物线吗?;
为常数)求点N的轨迹仍为抛物线吗?;
10. 设a、b、c均为实数,求证: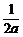 +
+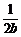 +
+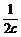 ≥
≥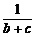 +
+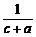 +
+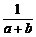 .
.
证明:∵a、b、c均为实数,
∴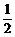 (
(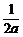 +
+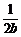 )≥
)≥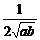 ≥
≥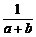 ,当a=b时等号成立;
,当a=b时等号成立;
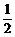 (
(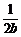 +
+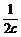 )≥
)≥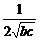 ≥
≥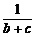 ,当b=c时等号成立;
,当b=c时等号成立;
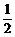 (
(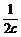 +
+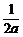 )≥
)≥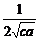 ≥
≥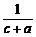 .
.
三个不等式相加即得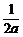 +
+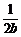 +
+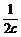 ≥
≥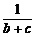 +
+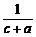 +
+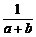 ,当且仅当a=b=c时等号成立.
,当且仅当a=b=c时等号成立.
[探索题](1).已知a3+b3=1,求a+b的取值范围.
(2) 已知a>0,b>0,a+b=4,求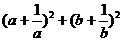 的最小值.
的最小值.
解(1) 易知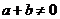 ,否则a=-b代入a3+b3=0与已知矛盾.
,否则a=-b代入a3+b3=0与已知矛盾.
令a+b=t≠0,由1=(a+b)3-3ab(a+b),得
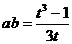 ,视a,b为方程
,视a,b为方程 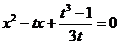 的根,
的根,
由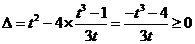 ,得
,得
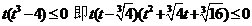 ①
①
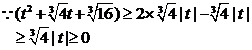
∴①为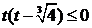
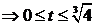
∴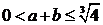
(2) 由4=a+b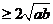 得ab≤4.
得ab≤4.
∴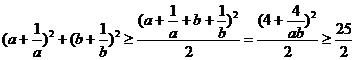
当且仅当a=b时取“=”,所求最小值为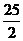 .
.
易错解:原式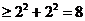 ,最小值为8.
,最小值为8.
9.某种生产设备购买时费用10万元,每年的设备管理费共计9千元,这种生产设备的维修费各年为:第一年2千元,第二年4千元,第三年6千元,依每年2千元的增量逐年递增,问这种生产设备最多使用多少年报废最合算?(即年平均费用最少)
解:设使用x年的年平均费用为y(万元),则
y=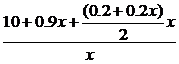 ≥1+2
≥1+2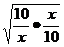 =3,
=3,
当且仅当x=10时,等号成立.
8.(1)若x>0,y>0,x+y=1,
求证:(1+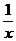 )(1+
)(1+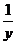 )≥9
)≥9
(2)设实数x,y满足y+x2=0,0<a<1,求证: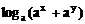 ≤
≤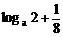 。
。
证明:(1)法一: 左边=(1+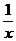 )(1+
)(1+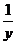 )=1+
)=1+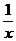 +
+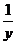 +
+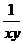 =1+
=1+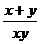 +
+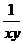
=1+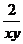 ≥1+
≥1+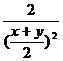 =9=右边 (当且仅当x=y=
=9=右边 (当且仅当x=y=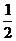 时取“=”号)
时取“=”号)
法二: 令x=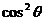 y=
y=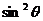 , 0<
, 0<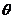 <
<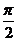
左边=(1+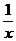 )(1+
)(1+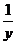 )=(1+
)=(1+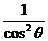 )(1+
)(1+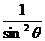 )
)
=1+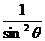 +
+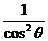 +
+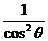 ·
·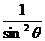 =1+
=1+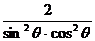
=1+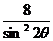 ≥1+8=9=右边
≥1+8=9=右边
0<2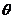 <
<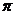
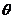 =
=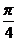 时,x=y=
时,x=y=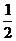 时取等号
时取等号
法三:∵x+y=1
∴左边=(1+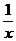 )(1+
)(1+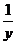 )=(1+
)=(1+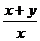 )(1+
)(1+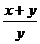 )=(2+
)=(2+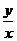 )(2+
)(2+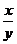 )
)
=5+2(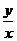 +
+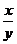 )≥5+4=9=右边 (当且仅当x=y=
)≥5+4=9=右边 (当且仅当x=y=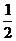 时取“=”号)
时取“=”号)
(2)∵ 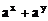 ≥
≥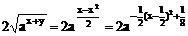 ,
,
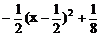 ≤
≤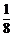 ,0<a<1
,0<a<1
∴ 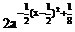 ≥
≥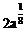 ∴
∴ 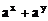 ≥
≥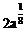
∴ 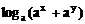 ≤
≤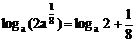
7. 设x≥0, y≥0, x2+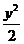 =1,求
=1,求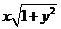 的最大值.
的最大值.
解法一: ∵x≥0, y≥0, x2+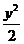 =1
=1
∴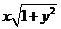 =
=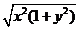 =
=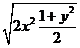
≤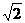
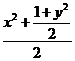 =
=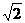
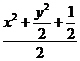 =
=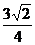
当且仅当x=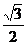 ,y=
,y=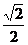 (即x2=
(即x2= 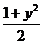 )时,
)时, 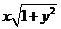 取得最大值
取得最大值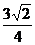
解法二: 令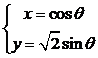 (0≤
(0≤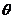 ≤
≤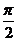 )
)
则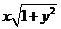 =cos
=cos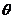
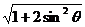 =
=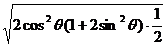
≤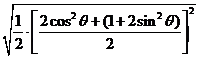 =
=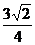
当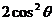 =
=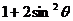 ,
,
即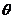 =
=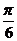 时,x=
时,x=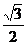 ,y=
,y=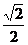 时,
时,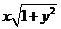 取得最大值
取得最大值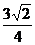
6.若x,y是正数,则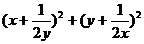 的最小值是_______
的最小值是_______
简答.提示:1-4.BBBB; 5. ②③; 6.原式=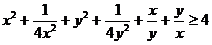
[解答题]
5. 下列不等式中恒成立的是_________
①ctgθ+tgθ≥2
②x+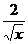 -1≥2
-1≥2
③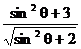 ≥2 ④xyz≤
≥2 ④xyz≤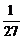 (x+y+z=1)
(x+y+z=1)
4.(2004全国I)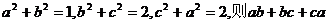 的最小值为( )
的最小值为( )
A.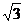 -
-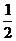 B.
B.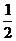 -
-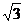 C.-
C.-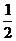 -
-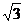 D.
D.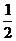 +
+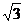
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com