
8.特殊角的三角函数值:
|
|
30° |
45° |
60° |
0° |
90° |
180° |
270° |
15° |
75° |
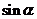 |
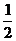 |
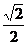 |
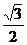 |
0 |
1 |
0 |
-1 |
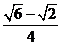 |
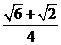 |
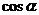 |
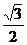 |
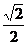 |
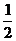 |
1 |
0 |
-1 |
0 |
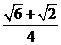 |
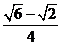 |
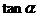 |
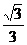 |
1 |
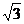 |
0 |
|
0 |
|
2-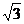 |
2+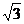 |
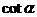 |
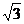 |
1 |
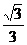 |
|
0 |
|
0 |
2+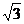 |
2-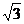 |
7.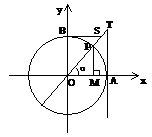 三角函数线的特征是:正弦线MP“站在
三角函数线的特征是:正弦线MP“站在 轴上(起点在
轴上(起点在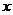 轴上)”、余弦线OM“躺在
轴上)”、余弦线OM“躺在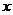 轴上(起点是原点)”、正切线AT“站在点
轴上(起点是原点)”、正切线AT“站在点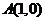 处(起点是
处(起点是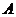 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如(1)若
)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如(1)若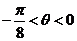 ,则
,则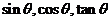 的大小关系为_____(答:
的大小关系为_____(答: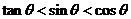 );(2)若
);(2)若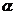 为锐角,则
为锐角,则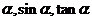 的大小关系为_______ (答:
的大小关系为_______ (答: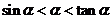 );(3)函数
);(3)函数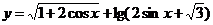 的定义域是_______(答:
的定义域是_______(答: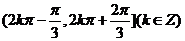 )
)
6、任意角的三角函数的定义:设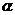 是任意一个角,P
是任意一个角,P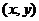 是
是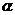 的终边上的任意一点(异于原点),它与原点的距离是
的终边上的任意一点(异于原点),它与原点的距离是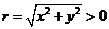 ,那么
,那么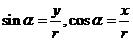 ,
,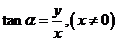 ,
,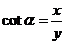
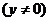 ,
,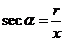
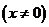 ,
,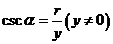 。三角函数值只与角的大小有关,而与终边上点P的位置无关。如(1)已知角
。三角函数值只与角的大小有关,而与终边上点P的位置无关。如(1)已知角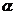 的终边经过点P(5,-12),则
的终边经过点P(5,-12),则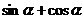 的值为__。(答:
的值为__。(答: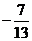 );(2)设
);(2)设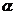 是第三、四象限角,
是第三、四象限角,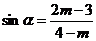 ,则
,则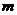 的取值范围是_______(答:(-1,
的取值范围是_______(答:(-1,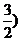 );(3)若
);(3)若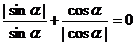 ,试判断
,试判断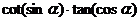 的符号(答:负)
的符号(答:负)
5.弧长公式: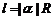 ,扇形面积公式:
,扇形面积公式: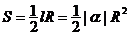 ,1弧度(1rad)
,1弧度(1rad)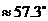 . 如已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。(答:2
. 如已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。(答:2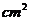 )
)
4、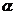 与
与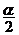 的终边关系:由“两等分各象限、一二三四”确定.如若
的终边关系:由“两等分各象限、一二三四”确定.如若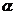 是第二象限角,则
是第二象限角,则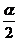 是第_____象限角(答:一、三)
是第_____象限角(答:一、三)
3. 终边相同的角的表示:
(1)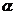 终边与
终边与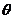 终边相同(
终边相同(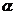 的终边在
的终边在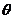 终边所在射线上)
终边所在射线上)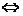
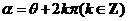 ,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角
,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角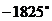 的终边相同,且绝对值最小的角的度数是___,合___弧度。(答:
的终边相同,且绝对值最小的角的度数是___,合___弧度。(答: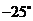 ;
;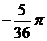 )
)
(2)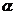 终边与
终边与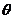 终边共线(
终边共线(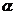 的终边在
的终边在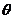 终边所在直线上)
终边所在直线上) 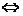
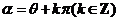 .
.
(3)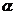 终边与
终边与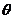 终边关于
终边关于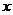 轴对称
轴对称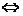
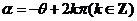 .
.
(4)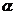 终边与
终边与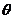 终边关于
终边关于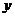 轴对称
轴对称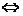
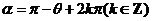 .
.
(5)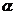 终边与
终边与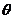 终边关于原点对称
终边关于原点对称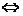
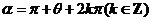 .
.
(6)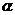 终边在
终边在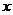 轴上的角可表示为:
轴上的角可表示为: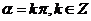 ;
;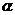 终边在
终边在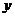 轴上的角可表示为:
轴上的角可表示为: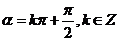 ;
;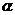 终边在坐标轴上的角可表示为:
终边在坐标轴上的角可表示为: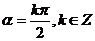 .如
.如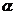 的终边与
的终边与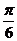 的终边关于直线
的终边关于直线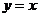 对称,则
对称,则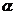 =____________。(答:
=____________。(答: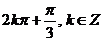 )
)
2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与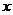 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。
(二).辨析用法
(1)搭配对象不同。如“交流”和“交换”,前者多与表示比较“虚”的一些事物的名词搭配,如交流体会,交流思想,交流感情等,后者则往往与表示“实”的一些事物的名词搭配,如交换场地,交换物品等。
(2)词性和语法功能也不同,如“诞辰”和“诞生”、“创见”和“创建”、“品位”和“品味”三组同义词,前者为名词,主要做主语、宾语,后者为动词,主要做谓语。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com