
3. 会书写常见弱电解质的电离方程式。
2. 了解电离平衡概念,能描述弱电解质在水溶液中的电离平衡。
1. 了解强电解质、弱电解质在水溶液中电离程度的差异,能判断常见的强电解质和弱电解质。
补充:求函数y=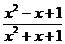 值域
值域
解:∵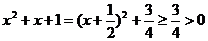 ,
,
∴函数的定义域R,原式可化为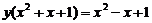 ,
,
整理得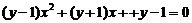 ,
,
若y=1,即2x=0,则x=0;
若y 1,∵
1,∵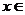 R,即有
R,即有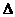
 0,
0,
∴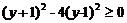 ,解得
,解得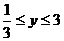 且 y
且 y 1.
1.
综上:函数是值域是{y|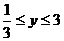 }.
}.
求函数值域的基本方法(直接法、换元法、判别式法);二次函数值域(最值)或二次函数在某一给定区间上的值域(最值)的求法.
1 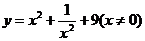 ;
;
解:∵x 0,
0,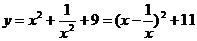 ,∴y
,∴y 11.
11.
另外,此题利用基本不等式解更简捷: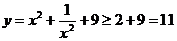
2 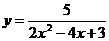
∵2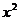 -4x+3>0恒成立(为什么?),
-4x+3>0恒成立(为什么?),
∴函数的定义域为R,
∴原函数可化为2y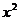 -4yx+3y-5=0,由判别式
-4yx+3y-5=0,由判别式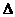
 0,
0,
即16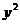 -4×2y(3y-5)=-8
-4×2y(3y-5)=-8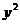 +40y
+40y 0(y
0(y 0),
0),
解得0 y
y 5,又∵y
5,又∵y 0, ∴0<y
0, ∴0<y 5.
5.
注意:利用判别式法要考察两端点的值是否可以取到.
3 求函数的值域
①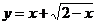 ;
②
;
②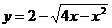
解:①令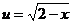
 0,则
0,则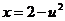 ,
,
原式可化为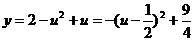 ,
,
∵u 0,∴y
0,∴y
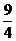 ,∴函数的值域是(-
,∴函数的值域是(- ,
,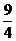 ].
].
②解:令 t=4x-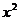
 0 得 0
0 得 0 x
x 4
4
在此区间内 (4x-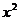 )
)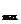 =4 ,(4x-
=4 ,(4x-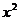 )
) =0
=0
∴函数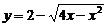 的值域是{ y| 0
的值域是{ y| 0 y
y 2}
2}
5.分段函数
 例5.求函数y=|x+1|+|x-2|的值域.
例5.求函数y=|x+1|+|x-2|的值域.
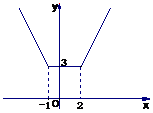
解法1:将函数化为分段函数形式: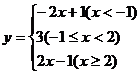 ,画出它的图象(下图),由图象可知,函数的值域是{y|y
,画出它的图象(下图),由图象可知,函数的值域是{y|y 3}.
3}.
解法2:∵函数y=|x+1|+|x-2|表示数轴上的动点x到两定点-1,2的距离之和,∴易见y的最小值是3,∴函数的值域是[3,+ ]. 如图
]. 如图
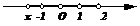
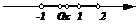
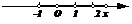
两法均采用“数形结合”,利用几何性质求解,称为几何法或图象法.
说明:以上是求函数值域常用的一些方法(观察法、配方法、判别式法、图象法、换元法等),随着知识的不断学习和经验的不断积累,还有如不等式法、三角代换法等.有的题可以用多种方法求解,有的题用某种方法求解比较简捷,同学们要通过不断实践,熟悉和掌握各种解法,并在解题中尽量采用简捷解法.
4.换元法
例4.求函数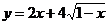 的值域
的值域
解:设 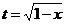 则 t
则 t 0 x=1-
0 x=1-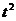
代入得 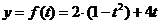
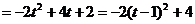
∵t 0 ∴y
0 ∴y 4
4
3.判别式法(△法):
判别式法一般用于分式函数,其分子或分母只能为二次式,解题中要注意二次项系数是否为0的讨论
例3.求函数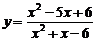 的值域
的值域
方法一:去分母得 (y-1)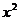 +(y+5)x-6y-6=0 ①
+(y+5)x-6y-6=0 ①
当 y¹1时 ∵xÎR
∴△=(y+5) +4(y-1)×6(y+1)
+4(y-1)×6(y+1) 0
0
由此得 (5y+1)
 0
0
检验 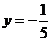 时
时 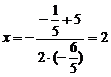 (代入①求根)
(代入①求根)
∵2 Ï 定义域 { x| x¹2且 x¹3} ∴
再检验 y=1 代入①求得 x=2 ∴y¹1
综上所述,函数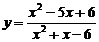 的值域为 { y| y¹1且
y¹
的值域为 { y| y¹1且
y¹ }
}
方法二:把已知函数化为函数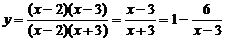 (x¹2)
(x¹2)
由此可得 y¹1 
∵ x=2时 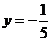 即
即

∴函数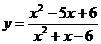 的值域为 { y| y¹1且
y¹
的值域为 { y| y¹1且
y¹ }
}
说明:此法是利用方程思想来处理函数问题,一般称判别式法. 判别式法一般用于分式函数,其分子或分母只能为二次式.解题中要注意二次项系数是否为0的讨论.
2.二次函数比区间上的值域(最值):
例2 求下列函数的最大值、最小值与值域:
①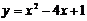 ;
;
②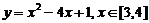 ;
;
③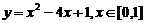 ; ④
; ④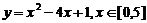 ;
;
解:∵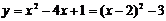 ,∴顶点为(2,-3),顶点横坐标为2.
,∴顶点为(2,-3),顶点横坐标为2.
①∵抛物线的开口向上,函数的定义域R,
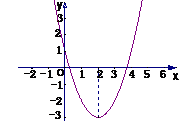 ∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y
∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y -3 }.
-3 }.
②∵顶点横坐标2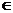 [3,4],
[3,4],
当x=3时,y= -2;x=4时,y=1;
∴在[3,4]上,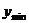 =-2,
=-2,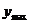 =1;值域为[-2,1].
=1;值域为[-2,1].
③∵顶点横坐标2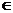 [0,1],当x=0时,y=1;x=1时,y=-2,
[0,1],当x=0时,y=1;x=1时,y=-2,
∴在[0,1]上,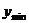 =-2,
=-2,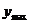 =1;值域为[-2,1].
=1;值域为[-2,1].
④∵顶点横坐标2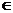 [0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
[0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
∴在[0,1]上,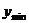 =-3,
=-3,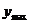 =6;值域为[-3,6].
=6;值域为[-3,6].
注:对于二次函数 ,
,
⑴若定义域为R时,
①当a>0时,则当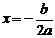 时,其最小值
时,其最小值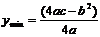 ;
;
②当a<0时,则当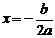 时,其最大值
时,其最大值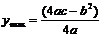 .
.
⑵若定义域为x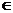 [a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
[a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
①若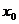
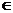 [a,b],则
[a,b],则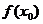 是函数的最小值(a>0)时或最大值(a<0)时,再比较
是函数的最小值(a>0)时或最大值(a<0)时,再比较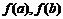 的大小决定函数的最大(小)值.
的大小决定函数的最大(小)值.
②若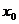
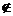 [a,b],则[a,b]是在
[a,b],则[a,b]是在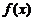 的单调区间内,只需比较
的单调区间内,只需比较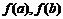 的大小即可决定函数的最大(小)值.
的大小即可决定函数的最大(小)值.
注:①若给定区间不是闭区间,则可能得不到最大(小)值;
②当顶点横坐标是字母时,则应根据其对应区间特别是区间两端点的位置关系进行讨论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com