
课时安排:两课时
第一课时
教学要点:
1、学习说明文知识
教学难点:
1 已知sina + sinb =
已知sina + sinb = 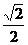 ,求cosa + cosb的范围
,求cosa + cosb的范围
解:设cosa + cosb = t,
则(sina + sinb)2 + (cosa + cosb)2= 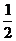 + t2
+ t2
∴2
+ 2cos(a - b) = 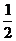 + t2 即 cos(a - b) =
+ t2 即 cos(a - b) = 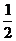 t2 -
t2 -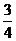
又∵-1≤cos(a - b)≤1 ∴-1≤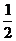 t2 -
t2 -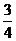 ≤1
≤1
∴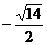 ≤t≤
≤t≤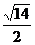
2 已知sin(a+b) =
已知sin(a+b) =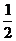 ,sin(a-b) =
,sin(a-b) = ,求
,求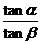 的值
的值
解:由题设: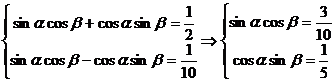
从而:
或设:x =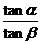 ∵
∵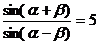
∴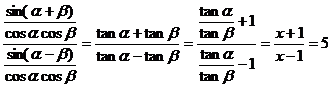
∴x =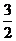 即
即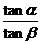 =
=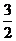
1 在△ABC中,已知cosA =
在△ABC中,已知cosA =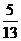 ,cosB =
,cosB =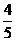 ,则cosC的值为( A )
,则cosC的值为( A )
(A)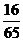 (B)
(B)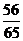 (C)
(C)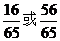 (D)
(D)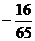
解:因为C = p - (A +
B), 所以cosC = - cos(A + B)
又因为A,BÎ(0, p), 所以sinA = 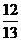 , sinB =
, sinB =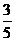 ,
,
所以cosC = - cos(A + B) =
sinAsinB - cosAcosB =

2 已知
已知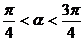 ,
, ,
,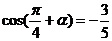 ,
,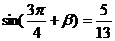 ,
,
求sin(a + b)的值
解:∵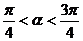 ∴
∴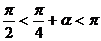
又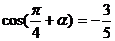 ∴
∴
∵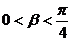 ∴
∴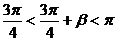
又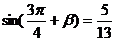 ∴
∴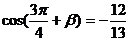
∴sin(a + b) = -sin[p + (a + b)] = 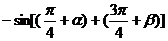
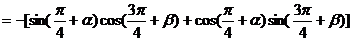
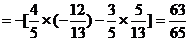
例1不查表,求下列各式的值:
1° sin75° 2° sin13°cos17°+cos13°sin17°
解:1°原式= sin(30°+45°)= sin30°cos45°+cos30°sin45°
=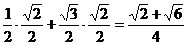
2°原式= sin(13°+17°)=sin30°=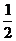
例2
求证:cosa+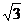 sina=2sin(
sina=2sin( +a)
+a)
证一(构造辅助角):
左边=2(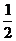 cosa+
cosa+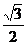 sina)=2(sin
sina)=2(sin cosa+cos
cosa+cos sina)
sina)
=2sin( +a)=右边
+a)=右边
证二:右边=2(sin cosa+cos
cosa+cos sina)=2(
sina)=2(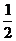 cosa+
cosa+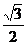 sina)
sina)
=
cosa+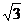 sina=左边
sina=左边
例3 已知sin(a+b)=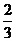 ,sin(a-b)=
,sin(a-b)=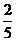 求
求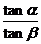 的值
的值
解: ∵sin(a+b)=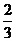 ∴sinacosb+cosasinb=
∴sinacosb+cosasinb=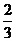 ①
①
|
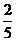 ∴sinacosb-cosasinb=
∴sinacosb-cosasinb=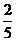 ②
②
①+②:sinacosb=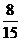
①-②:cosasinb=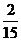
两角和与差的正弦
1 推导sin(a+b)=cos[
推导sin(a+b)=cos[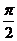 -(a+b)]=cos[(
-(a+b)]=cos[(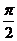 -a)-b]
-a)-b]
=cos(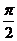 -a)cosb+sin(
-a)cosb+sin(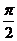 -a)sinb
-a)sinb
=sinacosb+cosasinb
即:
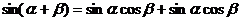 (Sa+b)
(Sa+b)
以-b代b得:  (Sa-b)
(Sa-b)
2 公式的分析,结构解剖,嘱记
公式的分析,结构解剖,嘱记
5.已知锐角a,b满足cosa=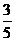 cos(a+b)=
cos(a+b)=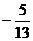 求cosb
求cosb
解:∵cosa=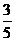 ∴sina=
∴sina=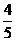
又∵cos(a+b)=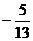 <0
<0
∴a+b为钝角
∴sin(a+b)=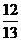
∴cosb=cos[(a+b)-a]=cos(a+b)cosa+sin(a+b)sina
= (角变换技巧)
(角变换技巧)
3.计算:cos65°cos115°-cos25°sin115°
解:原式= cos65°cos115°-sin65°sin115°=cos(65°+115°)=cos180°=-1
4 计算:-cos70°cos20°+sin110°sin20°
计算:-cos70°cos20°+sin110°sin20°
原式=-cos70°cos20°+sin70°sin20°=-cos(70°+20°)=0
2.求cos75°的值
解:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°
=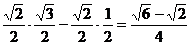
1.两角和与差的余弦公式:
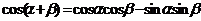
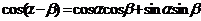
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com