
2.计算:
 (1)(0.027)
(1)(0.027) --2+
--2+ -(-1)0;
-(-1)0;

 (2)
·
(2)
·
解:(1)原式= -(-1)2-2+ -1
=-49+-1=-45.
(2)原式= ·
· ·
· ·
· ·
· =a0·b0=.
=a0·b0=.
|
题组二 |
指数函数的图象及应用 |
1.()+的值为 ( )
A.0 B. C. D.

 解析:() +
解析:() +
=[()3] -
-
=-=0.
答案:A
20.(本小题满分14分)
w已知直线 经过椭圆
经过椭圆 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆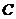 的右顶点为
的右顶点为 ,点
,点 是椭圆
是椭圆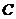 上位于
上位于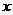 轴上方的动点,直线
轴上方的动点,直线 与直线
与直线 分别交于
分别交于 两点.
两点.
(1)求椭圆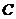 的方程;
的方程;
(2)求线段MN的长度的最小值;
 (3)当线段MN的长度最小时,在椭圆
(3)当线段MN的长度最小时,在椭圆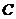 上是否存在这样的点
上是否存在这样的点 ,使得
,使得 的面积为
的面积为 ?若存在,确定点
?若存在,确定点 的个数,若不存在,说明理由.
的个数,若不存在,说明理由.
.w.w.k.s.5. m 2011届韶关市高三数学摸底测试卷 (文科)
19.(本小题满分14分)
设 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的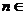 N
N ,都有
,都有
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比 ,数列
,数列 满足
满足
 ,
,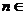 N
N
 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和 .
.
18.(本小题满分14分)
已知函数 (
( 、
、 ∈R,
∈R, ≠0),函数
≠0),函数 的图象在点(2,
的图象在点(2,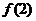 )处的切线与
)处的切线与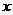 轴平行.
轴平行.
(1)用关于 的代数式表示
的代数式表示 ;
;
(2)求函数 的单调增区间.
的单调增区间.
17.(本小题满分14分)
盒子内装有10张卡片,分别写有1-10的10个整数,从盒子中任取1张卡片,记下它的读数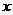 ,然后放回盒子内,第二次再从盒子中任取1张卡片,记下它的读数
,然后放回盒子内,第二次再从盒子中任取1张卡片,记下它的读数 .试求:
.试求:
(1) 是10的倍数的概率;
是10的倍数的概率;
(2) 是3的倍数的概率.
是3的倍数的概率.
16.(本小题满分12分)
如图,在直三棱柱 中,AC=3,
BC=4,AB=5,
中,AC=3,
BC=4,AB=5, ,点D是AB的中点。
,点D是AB的中点。
 (1)求证:
(1)求证: ;
;
(2)求证: ∥平面
∥平面 .
.
15.(本小题满分12分)
已知函数 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)求 的单调区间.
的单调区间.
14.若直线 与圆
与圆 相交于P、Q两点,且点P、Q关于直线
相交于P、Q两点,且点P、Q关于直线 对称,则不等式组
对称,则不等式组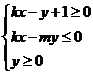 表示的平面区域的面积为________.
表示的平面区域的面积为________.
13.在棱长为 的正方体
的正方体 内任取一点P,则点P到点A的距离小于等于
内任取一点P,则点P到点A的距离小于等于
的概率为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com