
2.设函数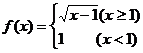 ,则
,则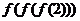 =
。
=
。
1.若函数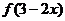 的定义域为[-1,2],则函数
的定义域为[-1,2],则函数 的定义域是
。
的定义域是
。
6.求下列极限: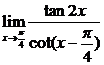
解:原式=
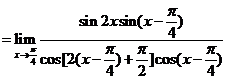 .
.
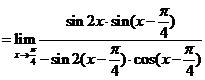
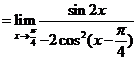
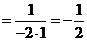

5.数列{an}满足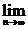 [(2n-1)an]=2.求
[(2n-1)an]=2.求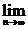 (nan)
(nan)
解: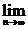 (nan)=
(nan)= 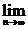 [(2n-1)an·
[(2n-1)an·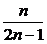 ]=
]=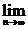 [(2n-1)an]·
[(2n-1)an]·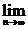
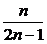
=2·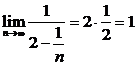 .
.
4.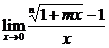 (m,n∈N*,n正奇数)
(m,n∈N*,n正奇数)
解:方法一: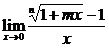
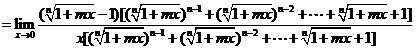
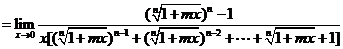
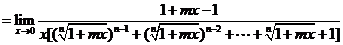
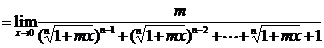
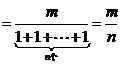
因为这里的m,n是确定数,不是无限数,所以在分母上,可以用函数极限的四则运算法则.
方法二:设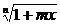 =y,则x=
=y,则x=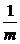 (yn-1)
(yn-1)
当x→0时,y→1.
∴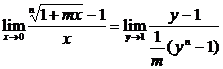
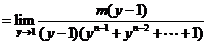
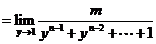
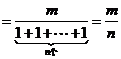
3.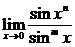 (m,n为自然数)
(m,n为自然数)
解: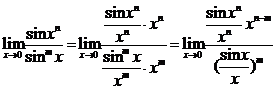
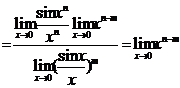
当n-m>0时,即n>m 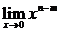 =0
=0
当n-m=0时,即n=m 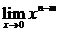 =1
=1
当n-m<0时,即n<m 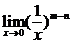 不存在.
不存在.
∴当n>m时,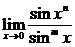 =0;当n=m时,
=0;当n=m时,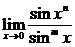 =1;
=1;
当n<m时,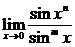 不存在.
不存在.
2.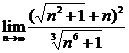
解: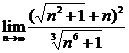
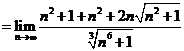
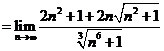
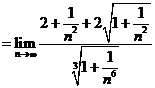
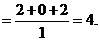
1. 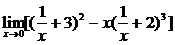
解: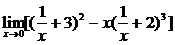
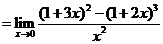
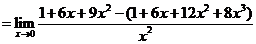
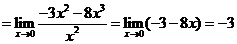
∴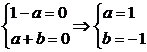
解:(2)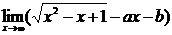
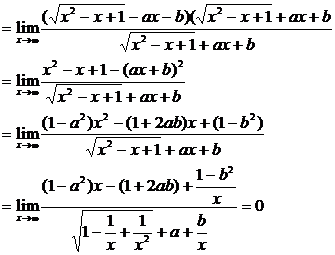
要使极限存在1-a2=0.
∴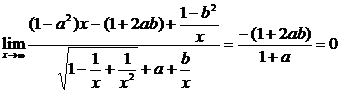
即1+2ab=0,a+1≠0.
∴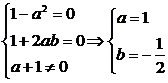
解:(3)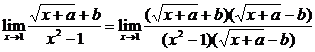
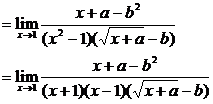
当x→1时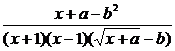 极限存在,则分子、分母必有公因式x-1. ∴a-b2=-1
极限存在,则分子、分母必有公因式x-1. ∴a-b2=-1
∴原式=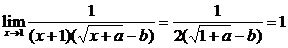
∴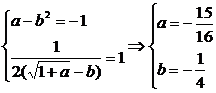
说明:第一题是分子分母同除以x的较低的幂,第二题是分子有理化,和第一题的方法相结合,第三题是因式分解法和分子有理化法相结合.
我们以前求极限的一种方法是分子、分母同除x的最高次幂,但像第一题,因为分子的次数低于分母的次数,如果分子除以x2,则分子极限为0,不符合,所以通分后,应除以分子分母中x的较低次幂.并且x的次数比分子x的最高次幂大的项的系数应该等于0,这样极限才存在.
例3 f(x)=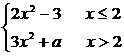 求a,使
求a,使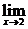 f(x)存在.
f(x)存在.
解:要使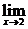 f(x)存在,则
f(x)存在,则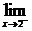 f(x)与
f(x)与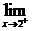 f(x)要存在且相等.
f(x)要存在且相等.
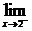 f(x)=
f(x)= 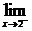 (2x2-3)=2·22-3=5.
(2x2-3)=2·22-3=5.
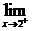 f(x)=
f(x)= 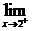 (3x2+a)=3·22+a=12+a.
(3x2+a)=3·22+a=12+a.
∴5=12+a.∴a=-7
例4设函数f(x)=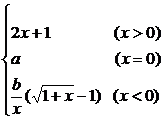 ,在x=0处连续,求a,b的值.
,在x=0处连续,求a,b的值.
分析:要使f(x)在x=0处连续,就要使f(x)在x=0处的左、右极限存在,并且相等,等于f(x)在x=0处的值a.
解: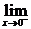 f(x)=
f(x)=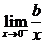 ·(
·(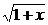 -1)
-1)
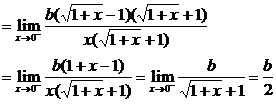
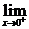 f(x)=
f(x)=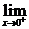 (2x+1)=2·0+1=1
(2x+1)=2·0+1=1
∴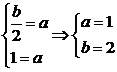
说明:这类连续的题目,也关键是求在一点处的左、右极限存在并都等于在这点的函数值,与函数在这点的极限存在的方法是相同的

例1 已知数列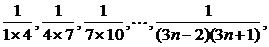 …
…
(1)计算S1,S2,S3,S4.
(2)猜想Sn的表达式,并证明.
(3)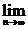 Sn.
Sn.
解:(1)S1=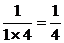 .
.
S2=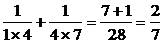
S3=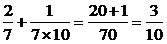
S4=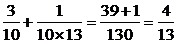 .
.
(2 )解:通项是以3n-2,3n+1两数乘积为分母的,而我们看到,在表示上面四个结果的分数中,分子可用项数n表示,分母可用3n+1表示,于是可猜想.
Sn=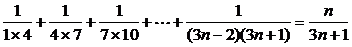
证明方法一:用数学归纳法证明如下:
1° 当n=1时,S1=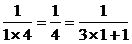 等式成立.
等式成立.
2° 假设当n=k时等式成立.即 Sk=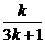 .
.
当n=k+1时.
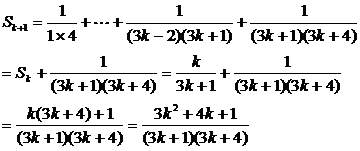
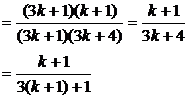
∴当n=k+1时,等式也成立.
∴Sn=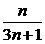 (n∈N*)
(n∈N*)
证明方法二: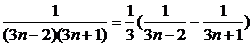
∴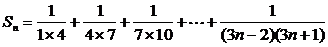
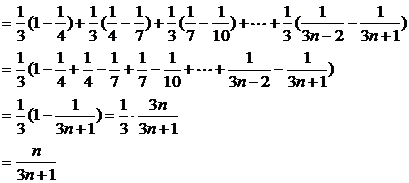
∴Sn=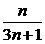
(3)解: 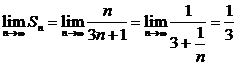
例2 已知下列极限,求a与b.
(1)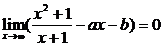
(2)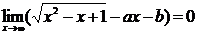
(3)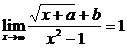
分析:此题属于已知x趋向于x0(或无穷大)时,函数的极限存在且等于某个常数,求函数关系式的类型.上边三个小题都不能简单地将x=x0直接代入函数的解析式中,因为(1)(2)中的x不趋于确定的常数,(3)虽然趋于1,但将x=1代入函数关系式中,分母为零.因此,解决此类问题的关键,是先要确定用哪种方法求极限,再将函数的解析式进行适当的变形,然后根据所给的条件进行分析,进而确定a,b的值.
解:(1)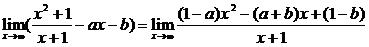
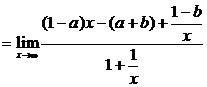
1° 如果1-a≠0,
∵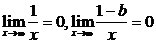
∴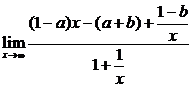 不存在.
不存在.
2° 如果 1-a=0,
∵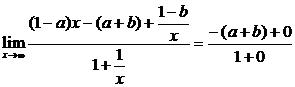
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com