
1. 在区间(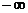 ,0)上为增函数的是( )
,0)上为增函数的是( )
A. 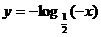 B.
B.
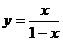
C. 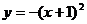 D.
D.
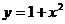
3. 周期性
[例6] 求下列函数是否为周期函数
(1)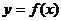 ,
,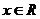 ,满足
,满足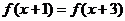
(2)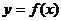 ,
,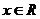 ,满足
,满足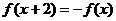
(3)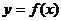 ,
,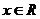 ,满足
,满足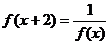
(4)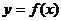 ,
,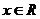 ,满足
,满足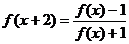
答案:
(1)令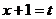 ∴
∴ 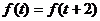 ∴
∴
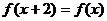
∴ T=2 周期函数
(2)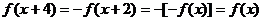
∴ T=4 周期函数
(3)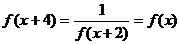 ∴ T=4
∴ T=4
(4)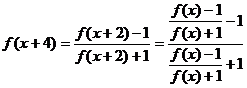
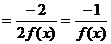
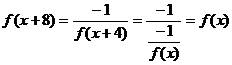 ∴ T=8
∴ T=8
[例7]
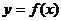 ,
,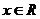 ,偶函数,
,偶函数,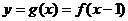 奇函数,则
奇函数,则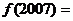 。
。
答案:
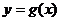 奇
奇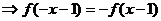
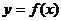 偶
偶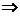
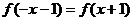
∴ 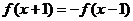 ∴
∴ 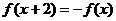 ∴
∴
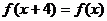
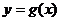 奇 ∴
奇 ∴ 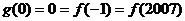
[例8]
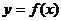 ,
,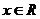 ,偶函数,周期函数,
,偶函数,周期函数, ,
,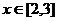 ,
,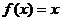 ,则
,则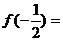
, ,
,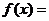 。
。
答案:
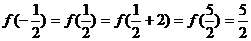

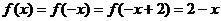
[模拟试题](答题时间:40分钟)
2. 单调性
[例4] 求下列函数的增区间
(1)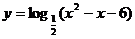
(2)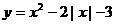
(3)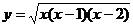
(4)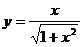
答案:
(1)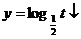
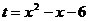 ∴
∴
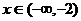
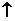
(2)作图
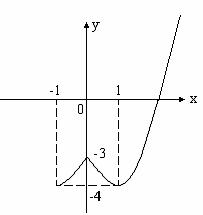
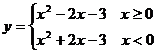 ∴
∴ 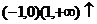
(3)令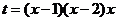
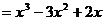
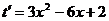
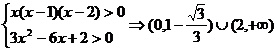
∴ 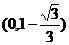 ,
,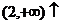
(4)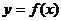 奇函数,
奇函数,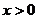 时,
时,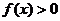
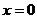 ,
,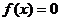 ,
,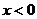 时,
时,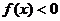
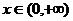
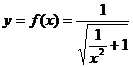 ∴
∴ 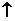 ∴ R上
∴ R上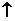
另解: ∴ R上
∴ R上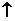
[例5](1)若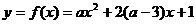 在区间
在区间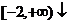 ,求
,求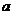 取值范围。
取值范围。
(2)若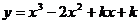 在(
在(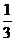 ,1)上
,1)上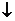 ,求
,求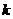 的取值范围。
的取值范围。
答案:
(1)① 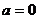 ,
,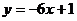 成立
成立
② 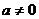
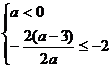
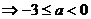 ∴
∴ 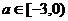
(2)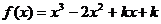
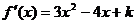
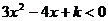 解集为A ∴
解集为A ∴ 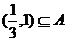
∴ 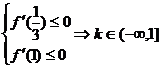
1. 奇偶性
[例1] 判断下列函数奇偶性
(1)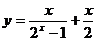
(2)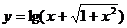
(3)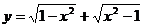
答案:
(1)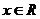 且
且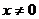 ,对称
,对称
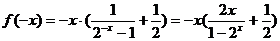
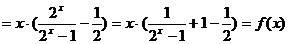
∴ 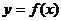 偶函数
偶函数
(2)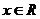 ,对称
,对称
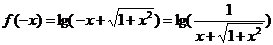
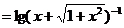
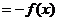
∴ 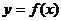 奇函数
奇函数
(3)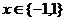 ,对称
,对称
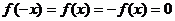
∴ 既奇又偶
[例2](1)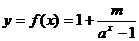 ,
,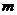 为何值时,
为何值时,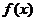 为奇函数
为奇函数
(2)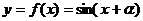 ,
,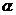 为何值时,
为何值时,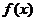 为偶函数
为偶函数
答案:
(1)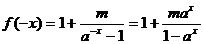
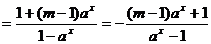
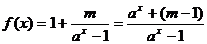
∴ 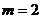 时,
时,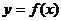 奇函数
奇函数
(2)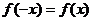
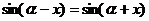
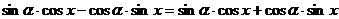
∴ 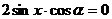 ∴
∴ 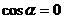
∴ 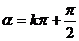
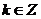
[例3]
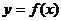 为R上偶函数,
为R上偶函数,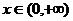 时
时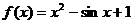 ,求
,求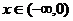 ,
,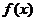 解析式。
解析式。
答案: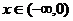
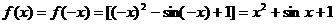
3. 周期性
对于函数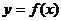 ,
,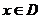
存在一个非0常数T,任取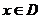
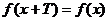 恒成立,那么
恒成立,那么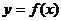 叫周期函数,T叫做周期。
叫周期函数,T叫做周期。
[典型例题]
2. 单调性
计算单调性的方法:定义法、复合函数法、图象法、导数法
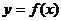
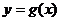
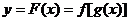
1. 奇偶性
(1)定义域A关于原点对称。任取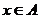
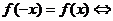 偶函数
偶函数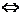 图象关于
图象关于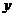 轴对称
轴对称
(2)定义域B关于原点对称,任取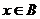
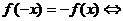 奇函数
奇函数 图象关于原点对称
图象关于原点对称
函数性质
18.(★★★★★)-Look!Someone has broken a glass.
-Well,it________ me I________ that.
A.wasn’t;didn’t do B.isn’t;haven’t done
C.wasn’t;hadn’t done D.isn’t;didn’t
17.(★★★★★)He paid no attention to my advice that he________ all the studying he had missed.
A.would make up for B.made for
C.make up for D.make his mark for
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com