
等效法是科学研究中常用的思维方法之一,它是从事物的等同效果这一基本点出发的,它可以把复杂的物理现象、物理过程转化为较为简单的物理现象、物理过程来进行研究和处理,其目的是通过转换思维活动的作用对象来降低思维活动的难度,它也是物理学研究的一种重要方法.
用等效法研究问题时,并非指事物的各个方面效果都相同,而是强调某一方面的效果.因此一定要明确不同事物在什么条件、什么范围、什么方面等效.在中学物理中,我们通常可以把所遇到的等效分为:物理量等效、物理过程等效、物理模型等效等.
6. 有一带负电的小球,其带电量q= - C。如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板B有一挡板要S,小球与挡板S的距离h=5cm,与A板距离H=45cm,重力作用不计。在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知k=
C。如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板B有一挡板要S,小球与挡板S的距离h=5cm,与A板距离H=45cm,重力作用不计。在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知k= ,而碰后小球的速度大小不变。
,而碰后小球的速度大小不变。
 (1)设匀强电场中挡板S所在位置的电势为零,则电场中P点的电势为多少?小球在P点时的电势能为多少?(电势能用E来表示)
(1)设匀强电场中挡板S所在位置的电势为零,则电场中P点的电势为多少?小球在P点时的电势能为多少?(电势能用E来表示)
(2)小球从P点出发第一次回到最右端的过程中电场力对小球做了多少功?
(3)小球经过多少次碰撞后,才能抵达A板?(取
例题解析:
例1.解析 小球从h0高处落地时,速率
第一次跳起时和又落地时的速率
第二次跳起时和又落地时的速率

第m次跳起时和又落地时的速率
 每次跳起的高度依次
每次跳起的高度依次 ,
,
通过的总路程

经过的总时间为

例2.(1)木板最初做匀速运动,由F=μMg解得,
第l 块铁块放上后,木板做匀减速运动,加速度大小为a1,即有:

代人数据解得:
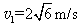
(2)设最终有n块铁块能静止在木板上.则木板运动的加速度大小为:

第1 块铁块放上后:
第2 块铁抉放上后:

第n块铁块放上后:
由上可得:
木板停下时, ,得n=6.6.即最终有7 块铁块放在木板上.
,得n=6.6.即最终有7 块铁块放在木板上.
(3)从放上第1块铁块至刚放上第7 块铁块的过程中,由(2)中表达式可得: 
从放上第7 块铁块至木板停止运动的过程中,设木板发生的位移为d ,则:

联立解得:
例3.(1)对A由动能定理: (1)
(1)
解得 ;A与B相碰后速度交换。
;A与B相碰后速度交换。
故第一次相碰后,A速度为零;B速度为 (2)
(2)
(2)从A开始运动到碰第一次历时t1=

设第二次碰前A速为 ,从第一次碰后到第二次碰前历时t2
,从第一次碰后到第二次碰前历时t2
对A、由动能定理: (3)
(3)
 (4) (2分)由(3)、(4)两式得:
(4) (2分)由(3)、(4)两式得:
故两球第二次碰时经历的时间为: (5)
(5)
(3)由(3)(4)两式解得:
此时B的速度为
第二次碰后速度再交换。由速度图像也可得到第三次碰前A速度


 (6)
(6)
此时B的速度为 (7)
(7)
依此类推第n次碰前A速度为:
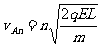 (8)
(8)
故第n次与第n+1次碰撞经历时间为:
 (9)
(9)
第n次碰后B以速度 匀速运动,
匀速运动,
故该时间内A通过的路程为: (10)
(10)
例4.解析 粒子进入磁场后做匀速圆周运动,经半周后通过x
轴进入电场后做匀减速直线运动,速度减为零后,又反向匀加
 速通过x轴进入磁场后又做匀速圆周运动,所以运动有周期性.
速通过x轴进入磁场后又做匀速圆周运动,所以运动有周期性.
它第3次到达x轴时距O点的距离L等于圆半径的4倍(如图
6-13甲所示)
粒子在磁场中做匀速圆周运动的半径为 
所以粒子射出时的速度 
粒子做圆周运动的半周长为 
粒子以速度v进入电场后做匀减速直线运动,能深入的最大距离为y,
因为
所以粒子在电场中进入一次通过的路程为 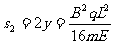
粒子第1次到达x轴时通过的路程为 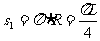
粒子第2次到达x轴时,已通过的路程为 
粒子第3次到达x轴时,已通过的路程为 
粒子第4次到达x轴时,已通过的路程为 
粒子第 次到达x轴时,已通过的路程为
次到达x轴时,已通过的路程为
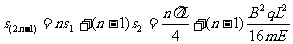
粒子第2n次到达x轴时,已通过的路程为 
上面n都取正整数.
例5.解析 当铅块向右运动时,铅块与10个相同的扁长木块中的第一块先发生摩擦力,若此摩擦力大于10个扁长木块与地面间的最大静摩擦力,则10个扁长木块开始运动,若此摩擦力小于10个扁长木块与地面间的最大摩擦力,则10个扁长木块先静止不动,随着铅块的运动,总有一个时刻扁长木块要运动,直到铅块与扁长木块相对静止,后又一起匀减速运动到停止.
铅块M在木块上滑行所受到的滑动摩擦力
设M可以带动木块的数目为n,则n满足:
即
上式中的n只能取整数,所以n只能取2,也就是当M滑行到倒数第二个木块时,剩下的两个木块将开始运动.设铅块刚离开第8个木块时速度为v,则

 得:
得: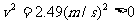
由此可见木块还可以滑到第9个木块上. M在第9个木块
上运动如图6-9甲所示,则对M而言有:
得:
第9及第10个木块的动力学方程为: ,
,
得:
设M刚离开第9个木块上时速度为 ,而第10个木块运动的速度为
,而第10个木块运动的速度为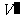 ,并设木块运动的距离为s,则M运动的距离为
,并设木块运动的距离为s,则M运动的距离为 ,有:
,有:


消去s及t求出: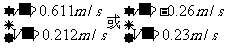 ,显然后一解不合理应舍去.
,显然后一解不合理应舍去.
因 ,故M将运动到第10个木块上.
,故M将运动到第10个木块上.
再设M运动到第10个木块的边缘时速度为 ,这时木块的速度为
,这时木块的速度为 ,则:
,则:

解得: ,故M不能滑离第10个木块,只能停在它的表面上,最后和木块一起静止在地面上.
,故M不能滑离第10个木块,只能停在它的表面上,最后和木块一起静止在地面上.
例6.(1)A在盒子内运动时,

由以上两式得 a=g
A在盒子内运动的时间 A在盒子外运动的时间
A在盒子外运动的时间
A从第一次进入盒子到第二次进入盒子的时间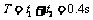
(2)小球在盒子内运动时,盒子的加速度
小球在盒子外运动时,盒子的加速度
小球运动一个周期盒子减少的速度为
从小球第一次进入盒子到盒子停下,小球运动的周期数为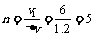
故要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个,即11个.
(3)小球第一次在盒内运动的过程中,盒子前进的距离为
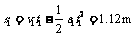
小球第一次从盒子出来时,盒子的速度
小球第一次在盒外运动的过程中,盒子前进的距离为
小球第二次进入盒子时,盒子的速度
小球第二次在盒子内运动的过程中,盒子前进的距离为
小球第二次从盒子出来时,盒子的速度
小球第二次在盒外运动的过程中,盒子前进的距离为
分析上述各组数据可知,盒子在每个周期内通过的距离为一等差数列,公差d=0.12m.且当盒子停下时,小球恰要进入盒内,最后0.2s内盒子通过的路程为0.04m.
所以从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程为

5.如图所示,有两本完全相同的书A、B,书重均为5N,若将两本书等分成若干份后,
交叉地叠放在一起,置于光滑的桌面上,并将书A通过一轻质弹簧秤与墙壁相连,用水平
向右的力F把书B抽出。现测得一组数据如下表:
|
实验次数 |
1 |
2 |
3 |
4 |
… |
n |
|
将书分成的份数 |
2 |
4 |
8 |
16 |
… |
逐页交叉 |
|
弹簧秤的示数(N) |
4.5 |
10.5 |
22.5 |
46.5 |
… |
190.5 |
 根据以上数据,试求:
根据以上数据,试求:
(1)若将书分成32份,弹簧秤的示数为多大?
(2)该书由多少张与首页大小相同的纸组成?
(3)如果两本书任意两张纸之间的动摩擦因数μ都相等,则μ为多大?
4.如图所示,R1=R3=R5=…=R99=5Ω,R2=R4=R6=…=R98=10Ω,R100=5Ω, =10V。求:
=10V。求:
(1)RAB=?
(2)电阻R2消耗的电功率应等于多少?
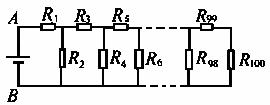 (3)
(3) 消耗的电功率;
消耗的电功率;
(4)电路上的总功率.
3.有n块质量均为m,厚度为d的相同砖块,平放在水平地面上,现将它们一块一块地叠放起来,如图所示,人至少做多少功?
2. 如图所示,一固定的斜面,倾角
如图所示,一固定的斜面,倾角 ,斜面长L=2.00米. 在斜面下端有一与斜面垂直的挡板. 一质量为m的质点,从斜面的最高点沿斜面下滑,初速度为零. 下滑到最底端与挡板发生弹性碰撞(无动能损失). 已知质点与斜面间的动摩擦因数
,斜面长L=2.00米. 在斜面下端有一与斜面垂直的挡板. 一质量为m的质点,从斜面的最高点沿斜面下滑,初速度为零. 下滑到最底端与挡板发生弹性碰撞(无动能损失). 已知质点与斜面间的动摩擦因数 ,试求此质点从开始到发生第11次碰撞的过程中运动的总路程.
,试求此质点从开始到发生第11次碰撞的过程中运动的总路程.

1.( )一物体放在光滑水平面上,初速为零,先对物体施加一向东的恒力F,历时1秒钟,随即把此力改为向西,大小不变,历时1秒钟,接着又把此力改为向东,大小不变,历时1秒钟,如此反复,只改变力的方向,共历时1分钟. 在此1分钟内
A.物体时而向东运动,时而向西运动,在1分钟末静止于初始位置之东
B.物体时而向东运动,时而向西运动,在1分钟末静止于初始位置
C.物体时而向东运动,时而向西运动,在1分钟末继续向东运动
D.物体一直向东运动,从不向西运动,在1分钟末静止于初始位置之东
例1.小球从高 处自由下落,着地后跳起又下落,每与地面相碰一次,速度减小
处自由下落,着地后跳起又下落,每与地面相碰一次,速度减小 ,求小球从下落到停止经过的总时间为通过的总路程.(g取10m/s2)
,求小球从下落到停止经过的总时间为通过的总路程.(g取10m/s2)
例2.如图所示,质量M=10kg、上表面光滑的足够长的木板的在F=50N的水平拉力作用下,以初速度v0=5m/s沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,将一铁块无初速地放在木板的最右端,当木板运动了L=1m时,又无初速地在木板的最右端放上第2块铁块,只要木板运动了L就在木板的最右端无初速放一铁块.试问.(取g=10m/s2)
(1)第1块铁块放上后,木板运动了L时,木板的速度多大?
(2)最终木板上放有多少块铁块?
 (3)最后一块铁块与木板右端距离多远?
(3)最后一块铁块与木板右端距离多远?
例3.如图所示,在足够大的光滑绝缘水平面上有两个质量均为m、相距为L的小球A和B均处于静止,小球A带+q的电量,小球B不带电。若沿水平向右的方向加一大小为E的匀强电场,A球将受力而运动,并与B球发生完全弹性碰撞(碰撞时间极短),碰后两球速度交换,若碰撞过程中无电荷转移,求:
(1)A与B第一次碰后瞬时B球的速率?
(2)从A开始运动到两球第二次相碰经历多长时间?
(3)两球从第n次碰撞到第n+1次碰撞时间内A球所通过的路程?

例4.如图所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B,在x轴下方有沿y轴负方向的匀强电场,场强为E. 一质量为m,电量为-q的粒子从坐标原点O
 沿着y轴方向射出. 射出之后,第三次到达x轴时,它与O点的距离为L. 求此粒子射出时的速度v和每次到达x轴时运动的总路程s.(重力不计)
沿着y轴方向射出. 射出之后,第三次到达x轴时,它与O点的距离为L. 求此粒子射出时的速度v和每次到达x轴时运动的总路程s.(重力不计)
例5.10个相同的扁长木块一个紧挨一个地放在水平
地面上,如图6-9所示,每个木块的质量 长度
长度
 ,它们与地面间的静摩擦因数和动摩擦因数均为
,它们与地面间的静摩擦因数和动摩擦因数均为

 原来木块处于静止状态. 左方第一个木块的左端
原来木块处于静止状态. 左方第一个木块的左端
上方放一个质量为M=1.0kg的小铅块,它与木块间的静摩
擦因数和动摩擦因数均为 现突然给铅块一向右的初速度
现突然给铅块一向右的初速度 ,使其在大木块上滑行. 试确定铅块最后的位置在何处(落在地上还是停在哪块木块上). 重力加速度g取
,使其在大木块上滑行. 试确定铅块最后的位置在何处(落在地上还是停在哪块木块上). 重力加速度g取 ,设铅块的长度与木块相比可以忽略.
,设铅块的长度与木块相比可以忽略.
例6.如图所示,A为位于一定高度处的质量为m、带电荷量为+q的小球,B为位于水平地面上的质量为M的用特殊材料制成的长方形空心盒子,且M=2m,盒子与地面间的动摩擦因数 =0.2,盒内存在着竖直向上的匀强电场,场强大小E=
=0.2,盒内存在着竖直向上的匀强电场,场强大小E= ,盒外没有电场.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=6 m/s的速度向右滑行.已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作用力大小相等方向相反.设盒子足够长,取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
,盒外没有电场.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=6 m/s的速度向右滑行.已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作用力大小相等方向相反.设盒子足够长,取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.

递推法是利用问题本身所具有的一种递推关系求解问题的一种方法,即当问题中涉及相互联系的物体或过程较多,相互作用或过程具有一定的重复性并且有规律时,应根据题目特点应用归纳的数学思想将所研究的问题归类,然后求出通式。 具体方法是先分析某一次作用的情况,得出结论;再根据多次作用的重复性和它们的共同点,把结论推广,然后结合数学知识求解。用递推法解题的关键是导出联系相邻两次作用的递推关系式。
10、一只老鼠从老鼠洞沿直线爬出,已知爬出速度v的大小与距洞口的距离s成反比,当老鼠到达洞口的距离s1=1m的A点时,速度大小为v1=20cm/s,当老鼠到达洞口的距离s2=2m的A点时,速度大小为v2为多少?老鼠从A点到达B点所用的时间t为多少?
例题解析:
例1.[解析] 电源的U-I图像是经常碰到的,由图线与纵轴的截距容易得出电动势E=1.5 V,图线与横轴的截距0.6 A是路端电压为0.80伏特时的电流,(学生在这里常犯的错误是把图线与横轴的截距0.6 A当作短路电流,而得出r=E/I短=2.5Ω 的错误结论.)故电源的内阻为:r=△U/△I=1.2Ω.
例2.[解析] 依题意在同一坐标系中作出分别从A、B站由不同时刻开出的汽车做匀速运动的s一t图像,如图所示.

从图中可一目了然地看出:(1)当B站汽车与A站第一辆汽车同时相向开出时,B站汽车的s一t图线CD与A站汽车的s-t图线有6个交点(不包括在t轴上的交点),这表明B站汽车在途中(不包括在站上)能遇到6辆从A站开出的汽车.(2)要使B站汽车在途中遇到的车最多,它至少应在A站第一辆车开出50 min后出发,即应与A站第6辆车同时开出此时对应B站汽车的s-t图线MN与A站汽车的s一t图线共有11个交点(不包括t轴上的交点),所以B站汽车在途中(不包括在站上)最多能遇到1l辆从A站开出的车.(3)如果B站汽车与A站汽车不同时开出,则B站汽车的s-t图线(如图中的直线PQ)与A站汽车的s-t图线最多可有12个交点,所以B站汽车在途中最多能遇到12辆车.
例3. [解析] 由图线可知:当U=100 V, I=0.32 A, P=UI=100×0.32=32 W;
定值电阻的阻值R=100 Ω
由UL+UR=100
V,得:UL+100I=100 V, I=
作该方程的图线(如图乙中直线),它跟原图线的交点的坐标为:I1=0.29 A,UL1=7l V;此交点就是灯泡的工作点,故灯泡消耗的实际功率:PL1=I1UL1≈20W.


例4. [解析]这是一道较好的力学综合题,涉及运动、力、功能关系的问题.粗看物理情景并不复杂,但题意直接给的条件不多,只能深挖题中隐含的条件.下图表达出了整个物理过程,可以从牛顿运动定律、运动学、图像等多个角度解出,应用图像方法,简单、直观.

作出速度一时间图像(如图a所示),位移为速度图线与时间轴所夹的面积,依题意,总位移为零,即△0AE的面积与△EBC面积相等,由几何知识可知△ADC的面积与△ADB面积相等,故△0AB的面积与△DCB面积相等(如图b所示).

即: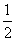 (v1×2t0)=
(v1×2t0)= 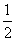 v2t0
v2t0
解得:v2=2v1
由题意知, 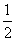 mv22=32J,故
mv22=32J,故 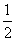 mv12=8J,
mv12=8J,
根据动能定理有 W1=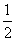 mv12=8J, W2=
mv12=8J, W2=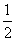 m(v22-v12)=24J
m(v22-v12)=24J
例5. [解析]在同一坐标系中作两物体做竖直上抛运动的s-t
[解析]在同一坐标系中作两物体做竖直上抛运动的s-t
图像,如图.要A、B在空中相遇,必须使两者相对于抛
出点的位移相等,即要求A、B图线必须相交,据此可从
图中很快看出:物体B最早抛出时的临界情形是物体B
落地时恰好与A相遇;物体B最迟抛出时的临界情形是
物体B抛出时恰好与A相遇.故要使A、B能在空中相遇,
△t应满足的条件为:2v0/g<△t<4v0/g
通过以上讨论可以看到,图像的内涵丰富,综合性比较强,而表达却非常简明,是物理学习中数、形、意的完美统一,体现着对物理问题的深刻理解.运用图像解题不仅仅是一种解题方法,也是一个感悟物理的简洁美的过程.
例6.[解析] 可将切割磁感应线的导体等效为电源按闭合电路来考虑,也可以直接用法拉第电磁感应定律按闭合电路来考虑.
当导线框部分进入磁场时,有恒定的感应电流,当整体全部进入磁场时,无感应电流,当导线框部分离开磁场时,又能产生相反方向的感应电流.所以应选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com