
61. 空间有几种距离?如何求距离?
点与点,点与线,点与面,线与线,线与面,面与面间距离。
将空间距离转化为两点的距离,构造三角形,解三角形求线段的长(如:三垂线定理法,或者用等积转化法)。
如:正方形ABCD-A1B1C1D1中,棱长为a,则:
(1)点C到面AB1C1的距离为___________;
(2)点B到面ACB1的距离为____________;
(3)直线A1D1到面AB1C1的距离为____________;
(4)面AB1C与面A1DC1的距离为____________;
(5)点B到直线A1C1的距离为_____________。

60. 三类角的定义及求法
(1)异面直线所成的角θ,0°<θ≤90°
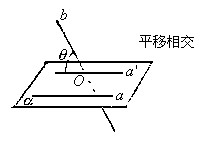
(2)直线与平面所成的角θ,0°≤θ≤90°
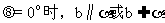

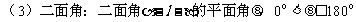
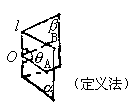
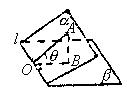
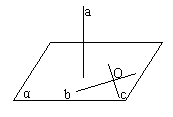
(三垂线定理法:A∈α作或证AB⊥β于B,作BO⊥棱于O,连AO,则AO⊥棱l,∴∠AOB为所求。)
三类角的求法:
①找出或作出有关的角。
②证明其符合定义,并指出所求作的角。
③计算大小(解直角三角形,或用余弦定理)。
[练习]
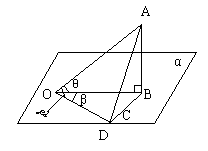
(1)如图,OA为α的斜线OB为其在α内射影,OC为α内过O点任一直线。

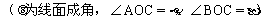
(2)如图,正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°。
①求BD1和底面ABCD所成的角;
②求异面直线BD1和AD所成的角;
③求二面角C1-BD1-B1的大小。
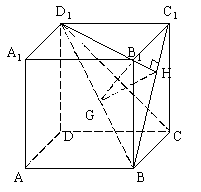
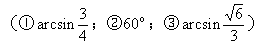
(3)如图ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,求面PAB与面PCD所成的锐二面角的大小。
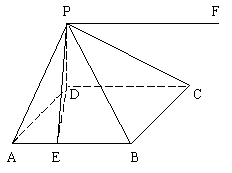
(∵AB∥DC,P为面PAB与面PCD的公共点,作PF∥AB,则PF为面PCD与面PAB的交线……)
59. 立体几何中平行、垂直关系证明的思路清楚吗?
平行垂直的证明主要利用线面关系的转化:

线面平行的判定:

线面平行的性质:
三垂线定理(及逆定理):
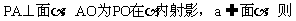
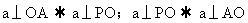

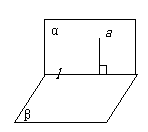
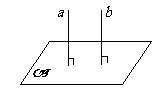
线面垂直:
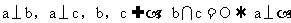
面面垂直:


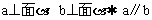

58. 线段的定比分点
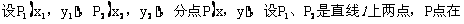
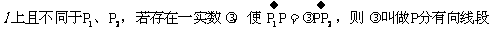
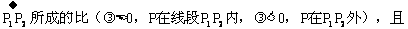

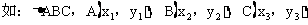
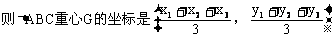
※. 你能分清三角形的重心、垂心、外心、内心及其性质吗?
57. 平面向量的数量积


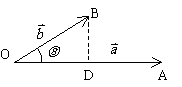
数量积的几何意义:
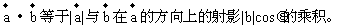
(2)数量积的运算法则

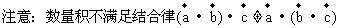
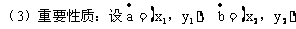
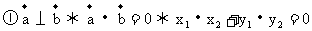

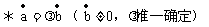

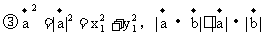
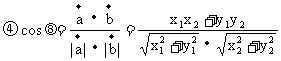
[练习]
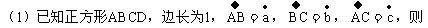
答案: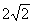
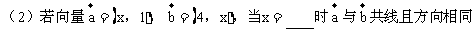
答案:2
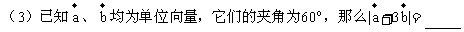
答案: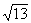
56. 你对向量的有关概念清楚吗?
(1)向量--既有大小又有方向的量。
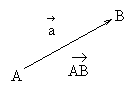


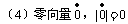

在此规定下向量可以在平面(或空间)平行移动而不改变。
(6)并线向量(平行向量)--方向相同或相反的向量。
规定零向量与任意向量平行。

(7)向量的加、减法如图:
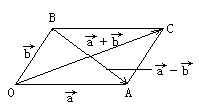
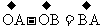
(8)平面向量基本定理(向量的分解定理)

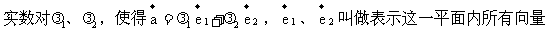
的一组基底。
(9)向量的坐标表示
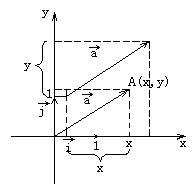

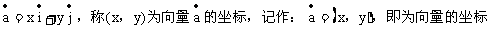
表示。
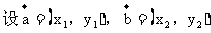
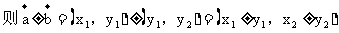
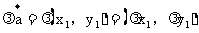
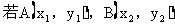
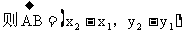
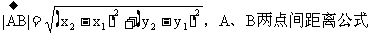
55. 对总体分布的估计--用样本的频率作为总体的概率,用样本的期望(平均值)和方差去估计总体的期望和方差。
要熟悉样本频率直方图的作法:

(2)决定组距和组数;
(3)决定分点;
(4)列频率分布表;
(5)画频率直方图。
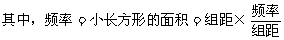
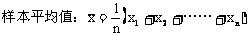
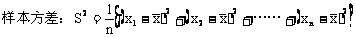
如:从10名女生与5名男生中选6名学生参加比赛,如果按性别分层随机抽样,则组成此参赛队的概率为____________。
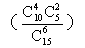
54. 抽样方法主要有:简单随机抽样(抽签法、随机数表法)常常用于总体个数较少时,它的特征是从总体中逐个抽取;系统抽样,常用于总体个数较多时,它的主要特征是均衡成若干部分,每部分只取一个;分层抽样,主要特征是分层按比例抽样,主要用于总体中有明显差异,它们的共同特征是每个个体被抽到的概率相等,体现了抽样的客观性和平等性。
53. 对某一事件概率的求法:
分清所求的是:(1)等可能事件的概率(常采用排列组合的方法,即


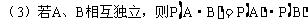
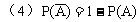
(5)如果在一次试验中A发生的概率是p,那么在n次独立重复试验中A恰好发生
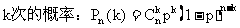
如:设10件产品中有4件次品,6件正品,求下列事件的概率。
(1)从中任取2件都是次品;
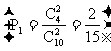
(2)从中任取5件恰有2件次品;
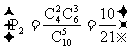
(3)从中有放回地任取3件至少有2件次品;
解析:有放回地抽取3次(每次抽1件),∴n=103
而至少有2件次品为“恰有2次品”和“三件都是次品”
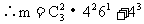
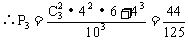
(4)从中依次取5件恰有2件次品。
解析:∵一件一件抽取(有顺序)
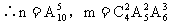
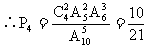
分清(1)、(2)是组合问题,(3)是可重复排列问题,(4)是无重复排列问题。
52. 你对随机事件之间的关系熟悉吗?
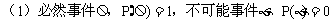
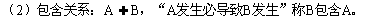

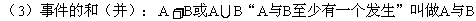 的和(并)。
的和(并)。
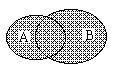
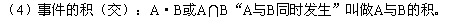
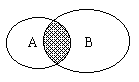
(5)互斥事件(互不相容事件):“A与B不能同时发生”叫做A、B互斥。

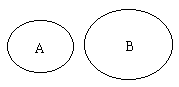
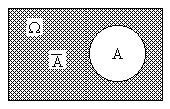
(6)对立事件(互逆事件):

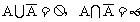
(7)独立事件:A发生与否对B发生的概率没有影响,这样的两个事件叫做相互独立事件。
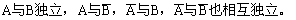
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com