
3.半角公式
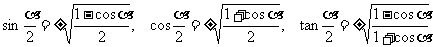
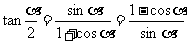
证:1°在 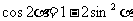 中,以a代2a,
中,以a代2a,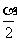 代a 即得:
代a 即得:
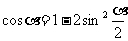 ∴
∴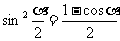
2°在 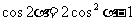 中,以a代2a,
中,以a代2a,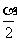 代a 即得:
代a 即得:
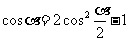 ∴
∴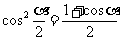
3°以上结果相除得: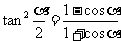
4° 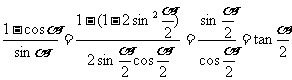
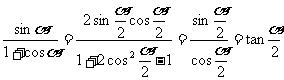
2.和差化积公式的推导
若令a + b = q,a - b = φ,则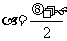 ,
,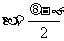 代入得:
代入得:
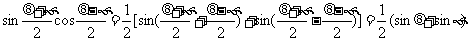
∴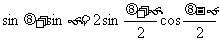
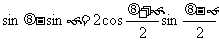
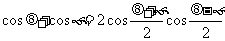

1.积化和差公式的推导
sin(a + b) + sin(a - b) = 2sinacosb
Þ sinacosb =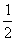 [sin(a + b) + sin(a - b)]
[sin(a + b) + sin(a - b)]
sin(a + b) - sin(a - b) = 2cosasinb
Þ cosasinb =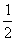 [sin(a + b) - sin(a - b)]
[sin(a + b) - sin(a - b)]
cos(a + b) + cos(a - b) = 2cosacosb
Þ cosacosb =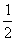 [cos(a + b) + cos(a - b)]
[cos(a + b) + cos(a - b)]
cos(a + b) - cos(a - b) = - 2sinasinb
Þ sinasinb = -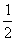 [cos(a + b) - cos(a - b)]
[cos(a + b) - cos(a - b)]
二倍角公式:
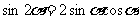 ;
;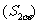
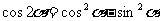 ;
;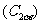
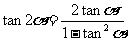 ;
;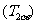
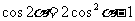
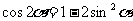

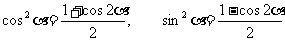
20.(16分)已知函数 (
(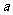 为实常数).
为实常数).
(1)若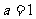 ,作函数
,作函数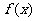 的图像;
的图像;
(2)设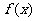 在区间
在区间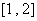 上的最小值为
上的最小值为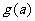 ,求
,求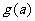 的表达式;
的表达式;
(3)设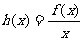 ,若函数
,若函数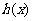 在区间
在区间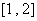 上是增函数,求实数
上是增函数,求实数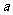 的取值范围.
的取值范围.
19.(16分)已知向量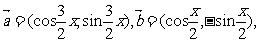 且
且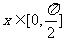 ,求:
,求:
(1) 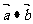 及
及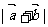 ;
;
(2) 若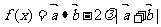 的最小值是
的最小值是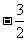 ,求
,求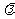 的值.
的值.
18.(15分)在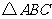 中,已知∠
中,已知∠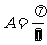 ,
, .设∠
.设∠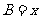 ,周长为
,周长为 .
.
(1) 求函数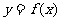 的解析式和定义域;
的解析式和定义域;
(2) 求 的最大值.
的最大值.
17.(15分)已知函数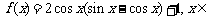 R.
R.
(1)求函数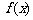 的最小正周期;
的最小正周期;
(2)求函数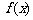 在区间
在区间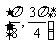 上的最小值和最大值.
上的最小值和最大值.
16.(14分)已知点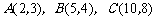 ,若
,若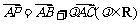 ,求当点
,求当点 在第二象限时,
在第二象限时,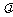 的取值范围.
的取值范围.
15. (14分)设非零向量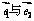 不共线
不共线
(1)如果 求证:A、B、D三点共线.
求证:A、B、D三点共线.
(2)若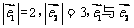 的夹角为
的夹角为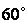 ,是否存在实数m,使得
,是否存在实数m,使得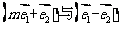 垂直?并说明理由
垂直?并说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com