
4.下列各句中加点成语使用恰当的一项 ( )

A. 李春晓老师热爱教育事业,几十年如一日,好为人师,为国家培养了大批英才。
B. 我觉得,在快节奏的现代化生活里,这种与荧屏相映成趣的电视化小说也许会大行其道。
C. 这些年轻的登山运动员决心以无所不为的勇气,克服重重困难,去征服珠穆朗玛峰。
D. 美国政府在台湾问题上的危言危行,只能搬起石头砸自己的脚。
3.下列各句中没有语病且句意明确的一句是( )
A.大家都有这样的经验,早晨脑子是最清醒的时候。
B.有些作品之所以屡屡出现错误,是因为作者思想水平低和文字功夫差等原因造成的。
C.我市药品食品监督部门已着手按照诚信度等级对全市食品生产企业进行分类管理,不良记录的多少,将直接影响企业的诚信等级
D.在当今这个竞争异常激烈的时代,任何一个企业家都不可能永远经历着辉煌而不面对挫折;遇到挫折并不可怕,可怕的是能否从失败的阴影中走出来。
2.下列各句横线处应填入的词句,最恰当的一组是( )
① 几年未见,那个头发乱莲蓬、小脸脏兮兮的外甥女娇娇,已经 得白白净净、亭亭玉立了,虽依旧亲热,但矜持了许多。
② 学生手中的课外读物五花八门,有的书籍内容和插图甚至低俗得让人
,这样的书籍对青少年的身心健康危害极大。
③ “3.19”大案发生后,专案组在圈定的几个嫌疑人被相继排除之后,只好采取大规模的摸排行动。经过半个月的排查,案情仍无进展。“
,
”正当案情陷入困境时,传来好消息:摸排人员发现了一条极其重要的线索。
A.出落 不堪入目 山重水复疑无路,柳暗花明又一村
B.保养 不忍卒读 山重水复疑无路,柳暗花明又一村
C.保养 不堪入目 踏破铁鞋无觅处,得来全不费功夫
D.出落 不忍卒读 踏破铁鞋无觅处,得来全不费功夫
1.下列各项中加点字的读音和书写全都正确的一项是( ) 
A.痉(jīng)挛 泾(jīng)渭分明 睚眦(cī)必报 怆(chuàng)然泪下
B.峻(jùn)工 不瘟(wēn)不火 锲(qiè)而不舍 怙恶不悛(quān)
C.癖(pǐ)好 谆(zhūn)谆告诫 淋漓尽至(zhì) 弱不禁(jīn)风
D.骇(hài)异 一抔(póu)黄土 矫揉(róu)造作 头晕目眩(xuàn)
(五)用递推方法解题
11、(03年全国)设{an}是首项为1的正项数列,且(n+1)a2n+1-nan2+an+1an=0,求它的通项公式是__1/n
12、(04年全国)已知数列{an}满足a.1=1,an=a1+2a2+3a3+---+(n-1)an-1
(n>1),则{an}的通项an=______a1=1;an= n
n 2
2
13、(04年北京)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列是等和数列,且,公和为5,那么的值为__3___,这个数列的前n项和的计算公式为__当n为偶数时,;当n为奇数时,
14. (04年全国)已知数列{an}中,a1=1,a2k=a2k-1+(-1)K,a2k+1=a2k+3k,其中k=1,2,3,…。
(1)求a3,a5; (2)求{an}的通项公式
解:(I)a2=a1+(-1)1=0, a3=a2+31=3.a4=a3+(-1)2=4 a5=a4+32=13, 所以,a3=3,a5=13.
(II) a2k+1=a2k+3k = a2k-1+(-1)k+3k, 所以a2k+1-a2k-1=3k+(-1)k,
同理a2k-1-a2k-3=3k-1+(-1)k-1, a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)+…+(a3-a1)
=(3k+3k-1+…+3)+[(-1)k+(-1)k-1+…+(-1)],
由此得a2k+1-a1= (3k-1)+
(3k-1)+ [(-1)k-1],
[(-1)k-1],
于是a2k+1= a2k=
a2k-1+(-1)k=
a2k=
a2k-1+(-1)k= (-1)k-1-1+(-1)k=
(-1)k-1-1+(-1)k= (-1)k=1.
(-1)k=1.
{an}的通项公式为:
当n为奇数时,an=
当n为偶数时,
(四)用函数方法解题
8、(04年天津)已知数列{an},那么“对任意的n N+,点Pn(n ,an)都在直线y=x+1上”是“{an}为等差数列”的( B)
N+,点Pn(n ,an)都在直线y=x+1上”是“{an}为等差数列”的( B)
A必要条件 B 充分条件 C 充要条件 D 既不充分也不必要条件
9、(99年上海)已知等差数列{an}满足3a4=7a7,且a1>0,Sn是{an}的前n项和,Sn取得最大值,则n=___9______.
10、(01年上海)已知数列{an}中an=2n-7,(n N+),
N+), +
+ +--+
+--+ =_153___
=_153___
(三)用整体化方法解题
5、(00年)已知等差数列{an}满足a1+a2+a3+…+a101=0,则有(C )
A a1+a101>0 B a2+a100<0 C a3+a99=0 D a51=51
6、(02年)若一个等差数列的前3项和为34,最后3项的和为146,且所有项的和为390,则这个数列的项数为(A)
A 13 B 12 C 11 D 10
7、(03年上海)在等差数列{an}中a5=3,a6=-2,a4+a5+…+a10=-49
(二)用赋值法解题
2、(96年)等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为(C )
A
130
B 170 C 210 D
260
3、(01年)设{an}是公比为q的等比数列, Sn是{an}的前n项和,若{Sn}是等差数列,则q=__1_
4、设数列{an}的前项的和Sn= (对于所有n
(对于所有n 1),且a4=54,则a1=__2___
1),且a4=54,则a1=__2___
(一)用基本量方法解题
1、(04年浙江)已知等差数列的公差为2,若a1,a3,a4成等比数列,则a2= (B )
A -4 B -6 C -8 D -10
例1.已知数列{a }是公差d≠0的等差数列,其前n项和为S
}是公差d≠0的等差数列,其前n项和为S .
.
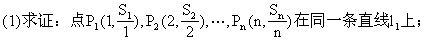

(2)过点Q (1,a
(1,a ),Q
),Q (2,a
(2,a )作直线12,设l
)作直线12,设l 与l
与l 的夹角为θ,
的夹角为θ,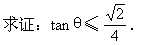

证明:(1)因为等差数列{a }的公差d≠0,所以
}的公差d≠0,所以
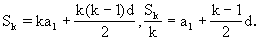

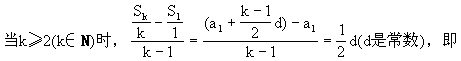

Kp p
p 是常数(k=2,3,…,n).
是常数(k=2,3,…,n).
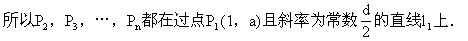

(2)直线l 的方程为y-a
的方程为y-a =d(x-1),直线l
=d(x-1),直线l 的斜率为d.
的斜率为d.
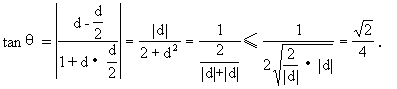

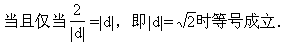

例2.已知数列 中,
中, 是其前
是其前 项和,并且
项和,并且 ,
,
⑴设数列 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
⑵设数列 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
⑶求数列 的通项公式及前
的通项公式及前 项和。
项和。
分析:由于{b }和{c
}和{c }中的项都和{a
}中的项都和{a }中的项有关,{a
}中的项有关,{a }中又有S
}中又有S =4a
=4a +2,可由S
+2,可由S -S
-S 作切入点探索解题的途径.
作切入点探索解题的途径.
解:(1)由S =4a
=4a ,S
,S =4a
=4a +2,两式相减,得S
+2,两式相减,得S -S
-S =4(a
=4(a -a
-a ),即a
),即a =4a
=4a -4a
-4a .(根据b
.(根据b 的构造,如何把该式表示成b
的构造,如何把该式表示成b 与b
与b 的关系是证明的关键,注意加强恒等变形能力的训练)
的关系是证明的关键,注意加强恒等变形能力的训练)
a -2a
-2a =2(a
=2(a -2a
-2a ),又b
),又b =a
=a -2a
-2a ,所以b
,所以b =2b
=2b ①
①
已知S =4a
=4a +2,a
+2,a =1,a
=1,a +a
+a =4a
=4a +2,解得a
+2,解得a =5,b
=5,b =a
=a -2a
-2a =3 ②
=3 ②
由①和②得,数列{b }是首项为3,公比为2的等比数列,故b
}是首项为3,公比为2的等比数列,故b =3·2
=3·2 .
.
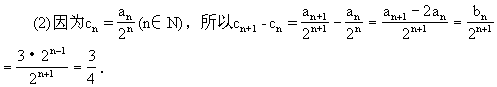

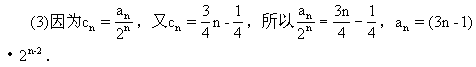
当n≥2时,S =4a
=4a +2=2
+2=2 (3n-4)+2;当n=1时,S
(3n-4)+2;当n=1时,S =a
=a =1也适合上式.
=1也适合上式.
综上可知,所求的求和公式为S =2
=2 (3n-4)+2.
(3n-4)+2.
说明:1.本例主要复习用等差、等比数列的定义证明一个数列为等差,等比数列,求数列通项与前 项和。解决本题的关键在于由条件
项和。解决本题的关键在于由条件 得出递推公式。
得出递推公式。
2.解综合题要总揽全局,尤其要注意上一问的结论可作为下面论证的已知条件,在后面求解的过程中适时应用.
例3.(04年浙江)设数列{an}的前项的和Sn= (an-1) (n
(an-1) (n +),(1)求a1;a2; (2)求证数列{an}为等比数列。
+),(1)求a1;a2; (2)求证数列{an}为等比数列。
解: (Ⅰ)由 ,得
,得 ∴
∴
 又
又 ,即
,即 ,得
,得 .
.
(Ⅱ)当n>1时,
得 所以
所以 是首项
是首项 ,公比为
,公比为 的等比数列.
的等比数列.
例4、(04年重庆)设a1=1,a2= ,an+2=
,an+2= an+1-
an+1- an (n=1,2,---),令bn=an+1-an (n=1,2---)求数列{bn}的通项公式,(2)求数列{nan}的前n项的和Sn。
an (n=1,2,---),令bn=an+1-an (n=1,2---)求数列{bn}的通项公式,(2)求数列{nan}的前n项的和Sn。
解:(I)因

故{bn}是公比为 的等比数列,且
的等比数列,且

(II)由


注意到 可得
可得
记数列 的前n项和为Tn,则
的前n项和为Tn,则



例5.在直角坐标平面上有一点列 ,对一切正整数
,对一切正整数 ,点
,点 位于函数
位于函数 的图象上,且
的图象上,且 的横坐标构成以
的横坐标构成以 为首项,
为首项, 为公差的等差数列
为公差的等差数列 。
。
⑴求点 的坐标;
的坐标;
⑵设抛物线列 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于 轴,第
轴,第 条抛物线
条抛物线 的顶点为
的顶点为 ,且过点
,且过点 ,记与抛物线
,记与抛物线 相切于
相切于 的直线的斜率为
的直线的斜率为 ,求:
,求: 。
。
⑶设 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是 中的最大数,
中的最大数, ,求
,求 的通项公式。
的通项公式。
解:(1)

(2) 的对称轴垂直于
的对称轴垂直于 轴,且顶点为
轴,且顶点为 .
. 设
设 的方程为:
的方程为:
把 代入上式,得
代入上式,得 ,
, 的方程为:
的方程为: 。
。
 ,
,


=
(3) ,
,


 T中最大数
T中最大数 .
.
设 公差为
公差为 ,则
,则 ,由此得
,由此得

说明:本例为数列与解析几何的综合题,难度较大(1)、(2)两问运用几何知识算出 ,解决(3)的关键在于算出
,解决(3)的关键在于算出 及求数列
及求数列 的公差。
的公差。
例6.数列 中,
中, 且满足
且满足

⑴求数列 的通项公式;
的通项公式;
⑵设 ,求
,求 ;
;
⑶设 =
=
 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意
,使得对任意 ,均有
,均有
 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1)由题意, ,
, 为等差数列,设公差为
为等差数列,设公差为 ,
,
由题意得 ,
, .
.
(2)若 ,
,

 时,
时,

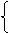 故
故


(3)




若 对任意
对任意 成立,即
成立,即 对任意
对任意 成立,
成立,
 的最小值是
的最小值是 ,
,
 的最大整数值是7。
的最大整数值是7。
即存在最大整数 使对任意
使对任意 ,均有
,均有
说明:本例复习数列通项,数列求和以及有关数列与不等式的综合问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com