
1. (2006上海) 如图,在平行四边形ABCD中,下列
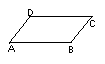
(2006上海) 如图,在平行四边形ABCD中,下列
结论中错误的是 ( )
(A) ;
(B)
;
(B) ;
;
(C) ; (D)
; (D) ;
;
5.平面向量的基本定理, 基底。
同步练习 5.1平面向量的概念与运算
[选择题]
4.两个向量共线定理,会由此定理证共线、求交点或线段长度,比值.
3.实数与向量的积
2.向量加法减法:
1.向量的有关概念: ①向量②零向量③单位向量④平行向量(共线向量)⑤相等向量
2.(2005全国Ⅰ) 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H, ,则实数m =
.是题(3)的结果.
,则实数m =
.是题(3)的结果.
[例4]一条河的两岸平行,河的宽度为 ,一艘船从
,一艘船从 处出发航行到河的正对岸
处出发航行到河的正对岸 处,船的航行速度为
处,船的航行速度为 ,水流速度为
,水流速度为 . (1)试求
. (1)试求 的夹角(精确到
的夹角(精确到 ),及船垂直到达对岸所用的时间(精确到
),及船垂直到达对岸所用的时间(精确到 ); (2)要使船到达对岸所用时间最少,
); (2)要使船到达对岸所用时间最少,  的夹角应为多少?
的夹角应为多少?
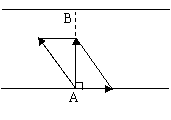 解(1)依题意,要使船到达对岸,就要使
解(1)依题意,要使船到达对岸,就要使 的合速度的方向正好垂直于对岸,所以
的合速度的方向正好垂直于对岸,所以 ,
,
 的夹角
的夹角 满足
满足 ,
, ,故
,故 的夹角
的夹角 ;船垂直到达对岸所用的时间
;船垂直到达对岸所用的时间 .
.
(2)设 的夹角为
的夹角为 (如图),
(如图), 在垂直方向上的分速度的和为
在垂直方向上的分速度的和为 ,而船到达对岸时,在垂直方向上行驶的路程为
,而船到达对岸时,在垂直方向上行驶的路程为 ,从而所
,从而所
用的时间为 ,显然,当
,显然,当 时,
时, 最小,即船头
最小,即船头
始终向着对岸时,所用的时间最少,为
 .
.
◆提炼方法:理解物理意义,用向量的知识解决.
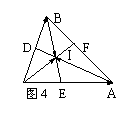 [研讨.欣赏]如图4,求证ΔABC的三条
[研讨.欣赏]如图4,求证ΔABC的三条
角平分,AD,BE,CF交于一点.
证明:设 ,CF,BE交于点I.由于
,CF,BE交于点I.由于
C,I,F共线, B,I,E共线,可设

由 得,
得,
∵ 不共线,∴
不共线,∴
同理设CF,AD交于点J, ,可求得δ=λ,即J与I重合,说明三条角平分线交于一点.
,可求得δ=λ,即J与I重合,说明三条角平分线交于一点.
◆方法提炼:相邻两边上单位向量的和向量在两边夹角角的平分线上.
2.证向量平行的方法:
(1)共线向量定理;(2)依定义; (3)用几何方法.
[例3]已知G是△ABC的重心,O是外心,H是垂心,P是平面ABC内任意一点,求证:
 (1)
(1)  ;
;
(2)  ;
;
(3)  ;
;
(4) 点O、G、H三点共线。
证明:(1)以向量 为邻边作平行
为邻边作平行
四边形GBEC,则 ,
,
又G为△ABC的重心知 ,从而
,从而 ,
,
∴ 。
。
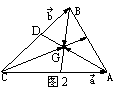
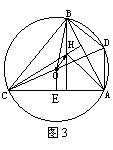
(2)如图1易知 ,
, ,
, ;
;
三式相加得

(3)作辅助线如图2,DA⊥AC,DB⊥BC,∴DA//BH,DB//AH
 在
在 ADBH中,
ADBH中, ,
,
∴
(4)在(2)中取P为O,得
∴ ,点O、G、H共线。
,点O、G、H共线。
◆提炼方法:1.明确解题目标,用好加法的两个法则、几何图形和向量中处理问题的一些手法,如向量共线、点共线的证法和用法;
[例1]如图,在梯形ABCD中
 ,G为对角线AC、BD的交点,E、
,G为对角线AC、BD的交点,E、
F分别是腰AD、BC的中点,求向量 。
。
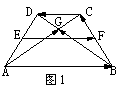 解:(1)∵ E,F分别是两腰的中点,
解:(1)∵ E,F分别是两腰的中点,
∴ ,又
,又
 ,
, ,
,
两式相加得;
(2)设 ,
, ,
,
由 得:
得:
∴ ,
,
◆提炼方法:1.用好“封闭折线的向量和等于零向量”;
2.由共线求交点的方法:待定系数λ,μ.
[例2]设 不共线,求证:点P、A、B共线的充要条件是:
不共线,求证:点P、A、B共线的充要条件是:
 。
。
证明:充分性:

∴A、P、B共线。
必要性:A、P、B共线,则有

必要性成立。
特例:当 时,
时, ,此时P为AB的中点,这是向量的中点公式。
,此时P为AB的中点,这是向量的中点公式。
◆提炼方法1. 利用向量证明三点共线的方法:
(1) 证明有公共点的的两个向量平行,则这两个向量的四个(三个)端点共线;
(2) 利用本题的结论.
7.( ) ,
) , .提示:作PC//OB,交AO延长线于点C,可知x<0.当
.提示:作PC//OB,交AO延长线于点C,可知x<0.当 时,PC//AB,设PC交OM于D,交AB延长线于E,P必在DE之间,可知
时,PC//AB,设PC交OM于D,交AB延长线于E,P必在DE之间,可知 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com