
7.若关于x的方程|x -6x+8|=a恰有两个不等实根,则实数a的取值范围是____________。
-6x+8|=a恰有两个不等实根,则实数a的取值范围是____________。
6. 对于满足0≤p≤4的所有实数p,使不等式x +px〉4x+p-3成立的x的取值范围是________。
+px〉4x+p-3成立的x的取值范围是________。
5.等差数列{a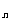 }中,a
}中,a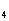 =84,前n项和为S
=84,前n项和为S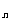 ,已知S
,已知S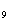 >0,S
>0,S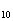 <0,则当n=______时,S
<0,则当n=______时,S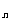 最大。
最大。
4.已知{a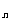 }是等比数列,且a
}是等比数列,且a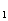 +a
+a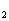 +a
+a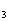 =18,a
=18,a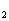 +a
+a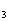 +a
+a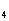 =-9,S
=-9,S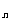 =a
=a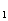 +a
+a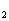 +…+a
+…+a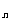 ,那么
,那么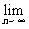 S
S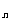 等于_____。
等于_____。
A. 8 B. 16 C. 32 D. 48
3.
已知函数f(x)=log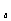 (x
(x -4x+8), x∈[0,2]的最大值为-2,则a=_____。
-4x+8), x∈[0,2]的最大值为-2,则a=_____。
A.  B.
B. 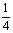 C. 2 D. 4
C. 2 D. 4
2.
已知函数f(x)=|2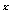 -1|,a<b<c,且f(a)>f(c)>f(b),则_____。
-1|,a<b<c,且f(a)>f(c)>f(b),则_____。
A. a<0,b<0,c>0 B. a<0,b>0,c>0 C. 2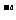 <2
<2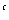 D. 2
D. 2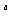 +2
+2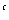 <2
<2
1. 方程sin2x=sinx在区间(0,2π)内解的个数是_____。
A. 1 B. 2 C. 3 D. 4
8. 建造一个容积为8m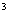 ,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为___________。
,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为___________。
[简解]1小题:图像法解方程,也可代入各区间的一个数(特值法或代入法),选C;
2小题:函数f(x)的对称轴为2,结合其单调性,选A;
3小题:从反面考虑,注意应用特例,选B;
4小题:设tg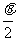 =x (x>0),则
=x (x>0),则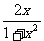 +
+ =
= ,解出x=2,再用万能公式,选A;
,解出x=2,再用万能公式,选A;
5小题:利用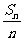 是关于n的一次函数,设S
是关于n的一次函数,设S =S
=S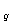 =m,
=m, =x,则(
=x,则(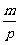 ,p)、(
,p)、(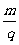 ,q)、(x,p+q)在同一直线上,由两点斜率相等解得x=0,则答案:0;
,q)、(x,p+q)在同一直线上,由两点斜率相等解得x=0,则答案:0;
6小题:设cosx=t,t∈[-1,1],则a=t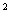 -t-1∈[-
-t-1∈[-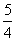 ,1],所以答案:[-
,1],所以答案:[-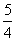 ,1];
,1];
7小题:设高h,由体积解出h=2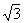 ,答案:24
,答案:24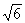 ;
;
8小题:设长x,则宽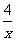 ,造价y=4×120+4x×80+
,造价y=4×120+4x×80+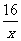 ×80≥1760,答案:1760。
×80≥1760,答案:1760。
Ⅱ、示范性题组:
例1. 设a>0,a≠1,试求方程log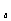 (x-ak)=log
(x-ak)=log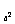 (x
(x -a
-a )有实数解的k的范围。(89年全国高考)
)有实数解的k的范围。(89年全国高考)
[分析]由换底公式进行换底后出现同底,再进行等价转化为方程组,分离参数后分析式子特点,从而选用三角换元法,用三角函数的值域求解。
[解]
将原方程化为:log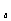 (x-ak)=log
(x-ak)=log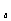
 , 等价于
, 等价于 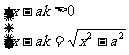 (a>0,a≠1)
(a>0,a≠1)
∴ k= -
-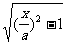 ( |
( | |>1 ),
|>1 ),
设 =cscθ, θ∈(-
=cscθ, θ∈(-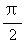 ,0)∪(0,
,0)∪(0, 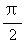 ),则 k=f(θ)=cscθ-|ctgθ|
),则 k=f(θ)=cscθ-|ctgθ|
当θ∈(-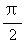 ,0)时,f(θ)=cscθ+ctgθ=ctg
,0)时,f(θ)=cscθ+ctgθ=ctg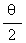 <-1,故k<-1;
<-1,故k<-1;
当θ∈(0, 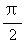 )时,f(θ)=cscθ-ctgθ=tg
)时,f(θ)=cscθ-ctgθ=tg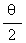 ∈(0,1),故0<k<1;
∈(0,1),故0<k<1;
综上所述,k的取值范围是:k<-1或0<k<1。
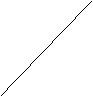   y
C
y
C   C C -ak -a a x |
[注] 求参数的范围,分离参数后变成函数值域的问题,观察所求函数式,引入新的变量,转化为三角函数的值域问题,在进行三角换元时,要注意新的变量的范围。一般地,此种思路可以解决有关不等式、方程、最大值和最小值、参数范围之类的问题。本题还用到了分离参数法、三角换元法、等价转化思想等数学思想方法。
另一种解题思路是采取“数形结合法”:
将原方程化为:log (x-ak)=log
(x-ak)=log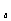
 ,等价于x-ak=
,等价于x-ak= (x-ak>0),设曲线C
(x-ak>0),设曲线C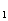 :y=x-ak,曲线C
:y=x-ak,曲线C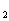 :y=
:y= (y>0),如图所示。
(y>0),如图所示。
由图可知,当-ak>a或-a<-ak<0时曲线C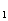 与C
与C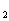 有交点,即方程有实解。所以k的取值范围是:k<-1或0<k<1。
有交点,即方程有实解。所以k的取值范围是:k<-1或0<k<1。
还有一种思路是直接解出方程的根,然后对方程的根进行讨论,具体过程是:原方程等价变形为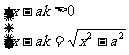 后,解得:
后,解得: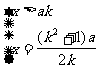 ,所以
,所以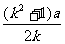 >ak,即
>ak,即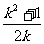 -k>0,通分得
-k>0,通分得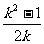 <0,解得k<-1或0<k<1。所以k的取值范围是:k<-1或0<k<1。
<0,解得k<-1或0<k<1。所以k的取值范围是:k<-1或0<k<1。
例2. 设不等式2x-1>m(x -1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
-1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
[分析]
此问题由于常见的思维定势,易把它看成关于x的不等式讨论。然而,若变换一个角度以m为变量,即关于m的一次不等式(x -1)m-(2x-1)<0在[-2,2]上恒成立的问题。对此的研究,设f(m)=(x
-1)m-(2x-1)<0在[-2,2]上恒成立的问题。对此的研究,设f(m)=(x -1)m-(2x-1),则问题转化为求一次函数(或常数函数)f(m)的值在[-2,2]内恒为负值时参数x应该满足的条件
-1)m-(2x-1),则问题转化为求一次函数(或常数函数)f(m)的值在[-2,2]内恒为负值时参数x应该满足的条件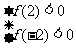 。
。
[解]问题可变成关于m的一次不等式:(x -1)m-(2x-1)<0在[-2,2] 恒成立,设f(m)=(x
-1)m-(2x-1)<0在[-2,2] 恒成立,设f(m)=(x -1)m-(2x-1),
-1)m-(2x-1),
则
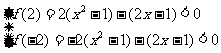
解得x∈(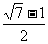 ,
,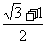 )
)
[注]
本题的关键是变换角度,以参数m作为自变量而构造函数式,不等式问题变成函数在闭区间上的值域问题。本题有别于关于x的不等式2x-1>m(x -1)的解集是[-2,2]时求m的值、关于x的不等式2x-1>m(x
-1)的解集是[-2,2]时求m的值、关于x的不等式2x-1>m(x -1)在[-2,2]上恒成立时求m的范围。
-1)在[-2,2]上恒成立时求m的范围。
一般地,在一个含有多个变量的数学问题中,确定合适的变量和参数,从而揭示函数关系,使问题更明朗化。或者含有参数的函数中,将函数自变量作为参数,而参数作为函数,更具有灵活性,从而巧妙地解决有关问题。
例3. 设等差数列{a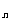 }的前n项的和为S
}的前n项的和为S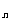 ,已知a
,已知a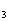 =12,S
=12,S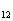 >0,S
>0,S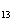 <0 。
<0 。
①.求公差d的取值范围; ②.指出S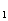 、S
、S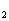 、…、S
、…、S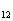 中哪一个值最大,并说明理由。(92年全国高考)
中哪一个值最大,并说明理由。(92年全国高考)
[分析]
①问利用公式a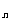 与S
与S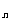 建立不等式,容易求解d的范围;②问利用S
建立不等式,容易求解d的范围;②问利用S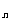 是n的二次函数,将S
是n的二次函数,将S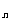 中哪一个值最大,变成求二次函数中n为何值时S
中哪一个值最大,变成求二次函数中n为何值时S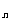 取最大值的函数最值问题。
取最大值的函数最值问题。
[解]①
由a =a
=a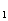 +2d=12,得到a
+2d=12,得到a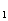 =12-2d,所以
=12-2d,所以
S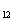 =12a
=12a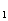 +66d=12(12-2d)+66d=144+42d>0,
+66d=12(12-2d)+66d=144+42d>0,
S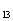 =13a
=13a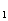 +78d=13(12-2d)+78d=156+52d<0。
+78d=13(12-2d)+78d=156+52d<0。
解得:-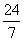 <d<-3。
<d<-3。
② S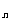 =na
=na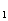 +
+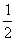 n(n1-1)d=n(12-2d)+
n(n1-1)d=n(12-2d)+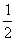 n(n-1)d
n(n-1)d
=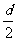 [n-
[n-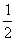 (5-
(5-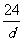 )]
)]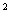 -
-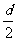 [
[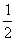 (5-
(5-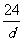 )]
)]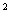
因为d<0,故[n-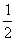 (5-
(5-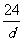 )]
)]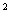 最小时,S
最小时,S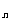 最大。由-
最大。由-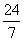 <d<-3得6<
<d<-3得6<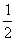 (5-
(5-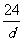 )<6.5,故正整数n=6时[n-
)<6.5,故正整数n=6时[n-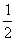 (5-
(5-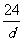 )]
)]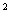 最小,所以S
最小,所以S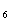 最大。
最大。
[注] 数列的通项公式及前n项和公式实质上是定义在自然数集上的函数,因此可利用函数思想来分析或用函数方法来解决数列问题。也可以利用方程的思想,设出未知的量,建立等式关系即方程,将问题进行算式化,从而简洁明快。由次可见,利用函数与方程的思想来解决问题,要求灵活地运用、巧妙的结合,发展了学生思维品质的深刻性、独创性。
本题的另一种思路是寻求a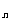 >0、a
>0、a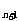 <0 ,即:由d<0知道a
<0 ,即:由d<0知道a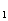 >a
>a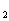 >…>a
>…>a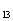 ,由S
,由S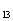 =13a
=13a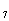 <0得a
<0得a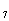 <0,由S
<0,由S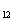 =6(a
=6(a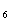 +a
+a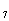 )>0得a
)>0得a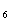 >0。所以,在S
>0。所以,在S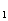 、S
、S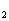 、…、S
、…、S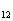 中,S
中,S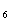 的值最大。
的值最大。
例4. 如图,AB是圆O的直径,PA垂直于圆O所在平面,C是圆周上任一点,设∠BAC=θ,PA=AB=2r,求异面直线PB和AC的距离。
[分析] 异面直线PB和AC的距离可看成求直线PB上任意一点到AC的距离的最小值,从而设定变量,建立目标函数而求函数最小值。
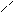 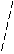       P
M
A
H
B
D C P
M
A
H
B
D C |
[解] 在PB上任取一点M,作MD⊥AC于D,MH⊥AB于H,
设MH=x,则MH⊥平面ABC,AC⊥HD 。
∴MD =x
=x +[(2r-x)sinθ]
+[(2r-x)sinθ] =(sin
=(sin +1)x
+1)x -4rsin
-4rsin θx+4r
θx+4r sin
sin θ
θ
=(sin θ+1)[x-
θ+1)[x-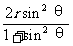 ]
] +
+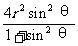
即当x=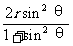 时,MD取最小值
时,MD取最小值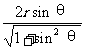 为两异面直线的距离。
为两异面直线的距离。
[注] 本题巧在将立体几何中“异面直线的距离”变成“求异面直线上两点之间距离的最小值”,并设立合适的变量将问题变成代数中的“函数问题”。一般地,对于求最大值、最小值的实际问题,先将文字说明转化成数学语言后,再建立数学模型和函数关系式,然后利用函数性质、重要不等式和有关知识进行解答。比如再现性题组第8题就是典型的例子。
例5. 已知△ABC三内角A、B、C的大小成等差数列,且tgA·tgC=2+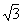 ,又知顶点C的对边c上的高等于4
,又知顶点C的对边c上的高等于4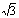 ,求△ABC的三边a、b、c及三内角。
,求△ABC的三边a、b、c及三内角。
[分析]已知了一个积式,考虑能否由其它已知得到一个和式,再用方程思想求解。
[解] 由A、B、C成等差数列,可得B=60°;
由△ABC中tgA+tgB+tgC=tgA·tgB·tgC,得
tgA+tgC=tgB(tgA·tgC-1)=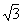 (1+
(1+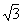 )
)
设tgA、tgC是方程x -(
-(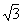 +3)x+2+
+3)x+2+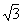 =0的两根,解得x
=0的两根,解得x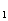 =1,x
=1,x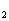 =2+
=2+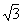
设A<C,则tgA=1,tgC=2+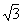 , ∴A=
, ∴A=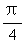 ,C=
,C=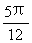
由此容易得到a=8,b=4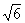 ,c=4
,c=4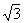 +4。
+4。
[注]本题的解答关键是利用“△ABC中tgA+tgB+tgC=tgA·tgB·tgC”这一条性质得到tgA+tgC,从而设立方程求出tgA和tgC的值,使问题得到解决。
例6. 若(z-x) -4(x-y)(y-z)=0,求证:x、y、z成等差数列。
-4(x-y)(y-z)=0,求证:x、y、z成等差数列。
[分析]
观察题设,发现正好是判别式b -4ac=0的形式,因此联想到构造一个一元二次方程进行求解。
-4ac=0的形式,因此联想到构造一个一元二次方程进行求解。
[证明] 当x=y时,可得x=z, ∴x、y、z成等差数列;
当x≠y时,设方程(x-y)t -(z-x)t+(y-z)=0,由△=0得t
-(z-x)t+(y-z)=0,由△=0得t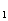 =t
=t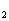 ,并易知t=1是方程的根。
,并易知t=1是方程的根。
∴t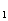 ·t
·t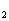 =
=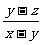 =1 , 即2y=x+z , ∴x、y、z成等差数列
=1 , 即2y=x+z , ∴x、y、z成等差数列
[注]一般地,题设条件中如果已经具备或经过变形整理后具备了“x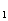 +x
+x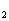 =a、x
=a、x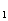 ·x
·x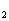 =b”的形式,则可以利用根与系数的关系构造方程;如果具备b
=b”的形式,则可以利用根与系数的关系构造方程;如果具备b -4ac≥0或b
-4ac≥0或b -4ac≤0的形式,可以利用根的判别式构造一元二次方程。这种方法使得非方程问题用方程思想来解决,体现了一定的技巧性,也是解题基本方法中的一种“构造法”。
-4ac≤0的形式,可以利用根的判别式构造一元二次方程。这种方法使得非方程问题用方程思想来解决,体现了一定的技巧性,也是解题基本方法中的一种“构造法”。
例7. △ABC中,求证:cosA·cosB·cosC≤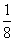 。
。
[分析]考虑首先使用三角公式进行变形,结合三角形中有关的性质和定理,主要是运用“三角形的内角和为180°”。变形后再通过观察式子的特点而选择和发现最合适的方法解决。
[证明]
设k=cosA·cosB·cosC= [cos(A+B)+cos(A-B)]·cosC=
[cos(A+B)+cos(A-B)]·cosC= [-cosC+cos(A-B)]cosC
[-cosC+cos(A-B)]cosC
整理得:cos C-cos(A-B)·cosC+2k=0,即看作关于cosC的一元二次方程。
C-cos(A-B)·cosC+2k=0,即看作关于cosC的一元二次方程。
∴ △=cos (A-B)-8k≥0 即 8k≤cos
(A-B)-8k≥0 即 8k≤cos (A-B)≤1
(A-B)≤1
∴ k≤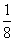 即cosA·cosB·cosC≤
即cosA·cosB·cosC≤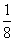
[注]本题原本是三角问题,引入参数后,通过三角变形,发现了其等式具有“二次”特点,于是联想了一元二次方程,将问题变成代数中的方程有实解的问题,这既是“方程思想”,也体现了“判别式法”、“参数法”。
此题的另外一种思路是使用“放缩法”,在放缩过程中也体现了“配方法”,具体解答过程是:cosA·cosB·cosC= [cos(A+B)+cos(A-B)]·cosC =-
[cos(A+B)+cos(A-B)]·cosC =- cos
cos C+
C+ cos(A-B)·cosC=-
cos(A-B)·cosC=- [cosC-
[cosC-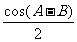 ]
] +
+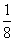 cos
cos (A-B)≤
(A-B)≤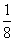 cos
cos (A-B) ≤
(A-B) ≤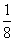 。
。
例8. 设f(x)=lg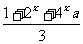 ,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
[分析]当x∈(-∞,1]时f(x)=lg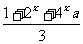 有意义的函数问题,转化为1+2
有意义的函数问题,转化为1+2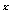 +4
+4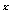 a>0在x∈(-∞,1]上恒成立的不等式问题。
a>0在x∈(-∞,1]上恒成立的不等式问题。
[解]
由题设可知,不等式1+2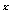 +4
+4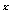 a>0在x∈(-∞,1]上恒成立,
a>0在x∈(-∞,1]上恒成立,
即:( )
)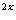 +(
+( )
)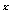 +a>0在x∈(-∞,1]上恒成立。
+a>0在x∈(-∞,1]上恒成立。
设t=( )
)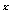 , 则t≥
, 则t≥ , 又设g(t)=t
, 又设g(t)=t +t+a,其对称轴为t=-
+t+a,其对称轴为t=-
∴ t +t+a=0在[
+t+a=0在[ ,+∞)上无实根, 即 g(
,+∞)上无实根, 即 g( )=(
)=( )
) +
+ +a>0,得a>-
+a>0,得a>-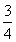
所以a的取值范围是a>-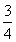 。
。
[注]对于不等式恒成立,引入新的参数化简了不等式后,构造二次函数利用函数的图像和单调性进行解决问题,其中也联系到了方程无解,体现了方程思想和函数思想。一般地,我们在解题中要抓住二次函数及图像、二次不等式、二次方程三者之间的紧密联系,将问题进行相互转化。
在解决不等式( )
)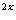 +(
+( )
)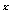 +a>0在x∈(-∞,1]上恒成立的问题时,也可使用“分离参数法”: 设t=(
+a>0在x∈(-∞,1]上恒成立的问题时,也可使用“分离参数法”: 设t=( )
)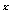 , t≥
, t≥ ,则有a=-t
,则有a=-t -t∈(-∞,-
-t∈(-∞,-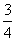 ],所以a的取值范围是a>-
],所以a的取值范围是a>-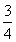 。其中最后得到a的范围,是利用了二次函数在某区间上值域的研究,也可属应用“函数思想”。
。其中最后得到a的范围,是利用了二次函数在某区间上值域的研究,也可属应用“函数思想”。
Ⅲ、巩固性题组:
7.正六棱锥的体积为48,侧面与底面所成的角为45°,则此棱锥的侧面积为___________。
6.关于x的方程sin x+cosx+a=0有实根,则实数a的取值范围是__________。
x+cosx+a=0有实根,则实数a的取值范围是__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com