
19.已知函数
1)若函数 在
在 处有极值
处有极值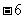 ,求
,求 的单调递减区间;
的单调递减区间;
2)若 的导数
的导数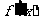 对
对 都有
都有 ,求
,求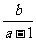 的取值范围.
的取值范围.
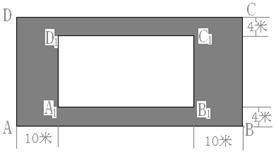
18.某房地产开发公司计划在一楼区内建造一个长方形公园 ,公园由长方形的休闲区
,公园由长方形的休闲区
和环公园人行道(阴影部分)组成。已知休闲区 的面积为
的面积为 平方米,人行道的宽分别
平方米,人行道的宽分别
 为
为 米和
米和 米(如图)(1)若设休闲区的长和宽的比
米(如图)(1)若设休闲区的长和宽的比
 ,求公园
,求公园 所占面积
所占面积 关于
关于 的函数
的函数 的解析式;(2)要使公园所占面积最小,休闲区
的解析式;(2)要使公园所占面积最小,休闲区 的长和宽(长>宽)该如何设计?
的长和宽(长>宽)该如何设计?
⒖已知点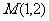 ,函数
,函数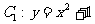 ,过点
,过点 作
作 的切线
的切线 ,
,
1)
求切线 的方程;
的方程;
2)
把函数 的图象向下平移1个单位得到曲线
的图象向下平移1个单位得到曲线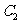 ,
,
求 与曲线
与曲线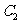 围成图形的面积.
围成图形的面积.
16.已知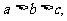
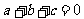 ,方程
,方程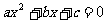 的两个实数根为
的两个实数根为 ,
,
1)求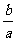 的取值范围; 2)若
的取值范围; 2)若 ,求
,求 的值. ( P104)
的值. ( P104)
⒘已知定义域为R的函数 是奇函数,其中
是奇函数,其中 是常数,且
是常数,且
1) 求 的值;
的值;
2)对任意的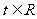 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
20、已知函数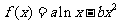 图象上一点
图象上一点 处的切线方程为
处的切线方程为
 . (Ⅰ)求
. (Ⅰ)求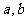 的值;
的值;
(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求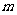 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, );
);
(Ⅲ)令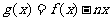 ,如果
,如果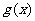 图象与
图象与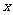 轴交于
轴交于 ,
, (
(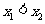 ),
), 中点为
中点为 ,求证:
,求证: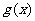 在
在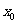 处的导数
处的导数 .
.
解:(Ⅰ) ,
, ,
,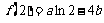 .
.
∴ ,且
,且 . …………………… 2分
. …………………… 2分
解得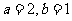 .
…………………… 3分
.
…………………… 3分
(Ⅱ) ,令
,令 ,
,
则 ,令
,令 ,得
,得 (
( 舍去).
舍去).
在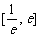 内,当
内,当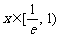 时,
时,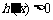 ,
∴
,
∴  是增函数;
是增函数;
当 时,
时,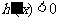 , ∴
, ∴  是减函数 …………………… 5分
是减函数 …………………… 5分
则方程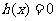 在
在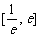 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是 …………7分
…………7分
即 . …………………………… 8分
. …………………………… 8分
(Ⅲ)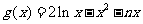 ,
, .
.
假设结论成立,则有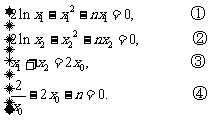 ………………………… 9分
………………………… 9分
①-②,得 .
.
∴ . …………………………………………………… 10分
. …………………………………………………… 10分
由④得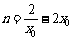 ,
,
∴ .即
.即 .
.
即 .⑤
…………………………………………………… 11分
.⑤
…………………………………………………… 11分
令 ,
, (
(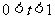 ), …………………………………… 12分
), …………………………………… 12分
则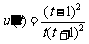 >0.∴
>0.∴ 在
在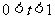 上增函数,
∴
上增函数,
∴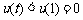 ,
……… 14分
,
……… 14分
∴⑤式不成立,与假设矛盾.
19、函数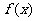 的定义域为
的定义域为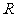 ,并满足条件:① 对任意
,并满足条件:① 对任意 ,有
,有 ;
;
② 对任意 ,有
,有 ;③
;③  .
.
(1)求 的值; (2)求证:
的值; (2)求证: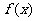 在
在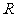 上是单调递增函数;
上是单调递增函数;
解:(1)令 ,则
,则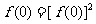

(2)任取 ,且
,且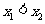
设 ,则
,则

 ,
,

 ,
,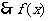 在
在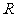 上是单调递增函数
上是单调递增函数
18、(14分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员
人(140< <420,且
<420,且 为偶数),每人每年可创利
为偶数),每人每年可创利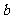 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利 万元,但公司需付下岗职员每人每年
万元,但公司需付下岗职员每人每年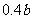 万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ,为获得最大的年经济效益,该公司应裁员多少人?
,为获得最大的年经济效益,该公司应裁员多少人?
解:设裁员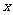 人,可获得的经济效益为
人,可获得的经济效益为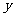 万元,则
万元,则
 =
=
依题意  ≥
≥ , ∴0<
, ∴0<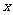 ≤
≤ .
.
又140< <420, 70<
<420, 70< <210.
<210.
① 当0< ≤
≤ ,即70<
,即70< ≤140时,
≤140时, ,
, 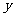 取到最大值;
取到最大值;
② 当 >
> ,即140<
,即140< <210时,
<210时, ,
, 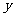 取到最大值;
取到最大值;
答:当70< ≤140时,应裁员
≤140时,应裁员 人;当140<
人;当140< <210时,应裁员
<210时,应裁员 人.
人.
17、(14分)已知函数f(x)=2x3+ax2+bx+3在x=-1和x=2处取得极值.
(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
解:(1)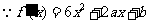
由已知有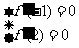 ,即
,即

 解得
解得

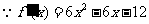
由 解得
解得 
由 解得
解得 
故函数f(x)在 和
和 是增函数,在
是增函数,在 上是减函数;
上是减函数;
当 时,有极大值10 , 当
时,有极大值10 , 当 时,有极小值
时,有极小值
(2)由(1)可知,要使f(x)在区间[m,m+4]上是单调函数时,须
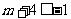 或
或  或
或

16、(12分)已知 ,设命题
,设命题 函数
函数 在
在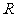 上单调递增,命题
上单调递增,命题 不等式
不等式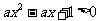 对
对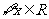 恒成立。若“
恒成立。若“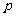 且
且 ”为假,“
”为假,“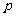 或
或 ”为真,求
”为真,求 的取值范围。
的取值范围。
解:由函数 在
在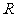 上单调递增,可得
上单调递增,可得
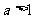
再由不等式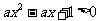 对
对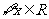 恒成立,可得
恒成立,可得


由于“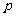 且
且 ”为假,“
”为假,“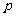 或
或 ”为真,故有
”为真,故有
 或
或


15、(12分)已知集合 ,
, ,若
,若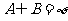 ,求实
,求实
数 的取值范围。
的取值范围。
解:
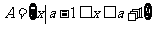 ,
,
又
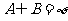 ,故有
,故有

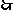
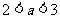
14、 3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com