
2.函数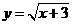 中,自变量
中,自变量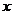 的取值范围是 .
的取值范围是 .
[命题意图]考查二次根式的意义
[参考答案]x≥-3
[试题来源]自编
1.分解因式: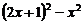 =
=
[命题意图]考查式的变形能力
[参考答案](3x+1)(x+1)
[试题来源]自编
4.估计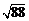 的大小应 ( )
的大小应 ( )
A.在9.1-9.2之间 B.在9.2-9.3之间 C.在9.3-9.4之间 D.在9.4-9.5之间
[命题意图]考查对数的估算
[参考答案]C
[试题来源]自编
3. 布袋中的5个红球与10个白球除颜色外完全相同,则从布袋中随机摸出一个球是白球概率为 ( )
A、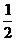 B、
B、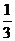 C、
C、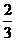 D、1
D、1
[命题意图]考查等可能事件的概率
[参考答案]C
[试题来源]自编
2. 神州7号运行1小时的行程约28 600 000 m,用科学记数法可表示为 ( )
A、0.286×108 m B、2.86×107 m C、28.6×106 m D、2.86×105 m
[命题意图]考查科学计数法
[参考答案]B
[试题来源]改编
1.下列计算中,正确的是( )
A.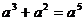 B.
B.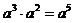 C.
C. D.
D.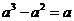
[命题意图]考查幂的运算法则
[参考答案]B
[试题来源]自编
28.如图11,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F.
(1)求梯形ABCD的面积;
(2)求四边形MEFN面积的最大值.
(3)试判断四边形MEFN能否为正方形,若能,求出
正方形MEFN的面积;若不能,请说明理由.
[命题意图]梯形的性质和图形的运动结合
[参考答案](1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H. ∵ AB∥CD,
 ∴ DG=CH,DG∥CH. ∴ 四边形DGHC为矩形,GH=CD=1.
∴ DG=CH,DG∥CH. ∴ 四边形DGHC为矩形,GH=CD=1.
∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴ △AGD≌△BHC. ∴ AG=BH=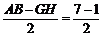 =3.
=3.
∵ 在Rt△AGD中,AG=3,AD=5, ∴ DG=4.
∴ 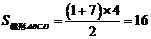 .
(3分)
.
(3分)
(2)∵ MN∥AB,ME⊥AB,NF⊥AB,
∴ ME=NF,ME∥NF. ∴ 四边形MEFN为矩形.
∵ AB∥CD,AD=BC, ∴ ∠A=∠B.
∵ ME=NF,∠MEA=∠NFB=90°,
∴ △MEA≌△NFB. ∴ AE=BF.
设AE=x,则EF=7-2x. ∵ ∠A=∠A,∠MEA=∠DGA=90°,
∴ △MEA∽△DGA. ∴ 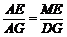 . ∴ ME=
. ∴ ME= .
(5分)
.
(5分)
∴ 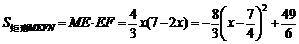 . 当x=
. 当x=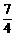 时,ME=
时,ME=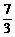 <4,
<4,
∴四边形MEFN面积的最大值为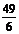 .
(7分)
.
(7分)
(3)能.由(2)可知,设AE=x,则EF=7-2x,ME= . 若四边形MEFN为正方形,
. 若四边形MEFN为正方形,
则ME=EF. 即 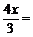 7-2x.解,得
7-2x.解,得 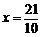 ∴ EF=
∴ EF=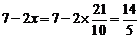 <4.
<4.
∴ 四边形MEFN能为正方形,其面积为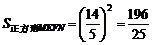 . (12分)
. (12分)
[试题来源]中考指南全真模拟试题
27. 如图,已知直线l:y=kx+2,k<0 ,与y轴交于点A,与x轴交于点B,以OA为直径的⊙P交l于另一点D,把弧AD沿直线l翻转后与OA交于点E。
(1)当k=-2时,求OE的长(4)分
(2)是否存在实数k,k<0 ,使沿直线l把弧AD翻转后所得的弧与OA相切?
若存在,请求出此时k的值,若不存在,请说明理由。(6)分
[命题意图]圆在坐标系的变换情况
[参考答案]答案:如图所示,由
∠DEO=∠EAD+∠ADE=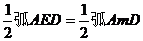 =∠AOD
=∠AOD
所以,OD=DE
当k=-2时,易得A(0,2),B(1,0),OA=2,OB=1,则AB=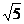
因为BO与⊙P切于点O,由切割线定理,得
OB2=BD·AB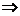 BD=
BD=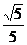 过点D作DC⊥AO于点C,则OE=2OC,DC∥OB 从而,有
过点D作DC⊥AO于点C,则OE=2OC,DC∥OB 从而,有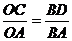
 故OE=
故OE=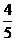
(2)假设存在实数k使得弧AD沿直线l翻转后所得弧与OA相切,则切点必为A,即E与A重合,由(1)知OD=AD。又∠ADO=90°,所以∠OAD=45°此时,OB=OA=2,B(2,0) ∴k=-1,
故存在k=-1,使得弧AD沿直l翻转后所得弧与OA相切。 (6)
[试题来源]2009北京中考模拟
26. .已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
[命题意图]二次函数和一元二次方程根与系数关系
[参考答案]解:1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2 ∴由抛物线的对称性可得点A的坐标为(-6,0)∴A、B、C三点的坐标分别是A(-6,0)、B(2,0)、C(0,8) (4分)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式y=ax2+bx+8,得
∴所求抛物线的表达式为y=-x2-x+8
[试题来源]本校月考加工总结所得
25. (本题满分10分) 如图10,一次函数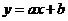 的图象与反比例函数
的图象与反比例函数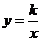 的图象交于M、N两点.
的图象交于M、N两点.
(1)求反比例函数和一次函数的解析式;
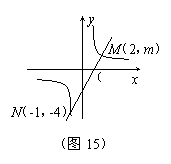 (2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
[命题意图]一次函数和反比例函数的综合应用
[参考答案](1)将N(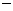 1,
1,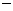 4)代入
4)代入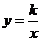 中 得k=4
(2分)
中 得k=4
(2分)
反比例函数的解析式为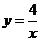
将M(2,m)代入解析式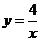 中 得m=2
(4
中 得m=2
(4
将M(2,2),N(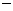 1,
1,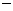 4)代入
4)代入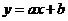 中
中
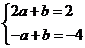 解得a=2 b=-2
(5分)一次函数解析式为
解得a=2 b=-2
(5分)一次函数解析式为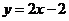
[试题来源]本校月考加工总结所得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com