
1. 作文动笔之前一般都要先打腹稿。在确立中心上、运用材料上、篇章结构上,充分酝酿。
8. 最后应注意复查全文。看内容要点有无遗漏,标点、格式、大小写是否规范,是否有语病等。
总之,要心有全局。英文写作如果结构意识良好,应试写作就简化成为一个填空的过程了,适当地填入观点、素材,文章就自然而然立起来了。临考在即,同学们要牢记英语写作的基本要领,特编顺口溜如下:细审题,巧构思,列要点,防遗漏。写日记,同汉语;书信、通知格式要牢记。看清图表细梳理,写人记事按顺序;完稿后查遗漏,整洁干净莫忘记。
英语作文写作“四步走”
由于时间限制,高考时一般在15分钟左右必须完成英语作文。高考的英语作文步骤如下:
7. 注意保持卷面整洁,书写工整清楚。书写的好坏会直接影响阅卷老师的情绪。
6. 注意文章的长度。看具体内容而定,如果内容多应多用复杂句式,如果内容不多,为了达到词的限数应多用简单句式,并适当增补合理内容。
5. 遇到一时想不起的词语,需变通。可以用同义近义词代替,也可以用否定词加反义词来表达,亦可变换句式。不可钻牛角尖,更不能生造词语,汉化表达。
4. 要刻意把好语言关。要用自己最熟悉的句型结构和词语,力求文理通顺,语言准确。没有把握的词句不要写,确有把握的的可以锦上添花。
3. 勿要直译,需意译。尤其对看图情景作文要构建完整故事结构,不可逐句罗列了事。
2. 列题纲使要点条理化,有序化,统筹安排布局。
1. 首先要认真审题。读懂题目所给信息,初步确定要点内容,并可用序号标出以免遗忘。
1.3.1利用导数判断函数的单调性
|
学习目标: 1.正确理解利用导数判断函数的单调性的原理; 2.掌握利用导数判断函数单调性的方法  学习重点难点: 利用导数判断函数单调性  . .自主学习 一、知识再现: 1. 函数的单调性. 对于任意的两个数x1,x2∈I,且当x1<x2时, 都有f(x1)<f(x2),那么函数f(x)就是区间I上的增函数. 对于任意的两个 数x1,x2∈I,且当x1<x2时,都有f(x1)>f(x2),那么函数f(x)就是区间 I上的减函数. 2. 导数的概念及其四则运算 二、新课探究: 1、定义:一般地,设函数y=f(x) 在某个区间内有导数,如果在 这个区间内 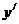 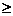 0,那么函数y=f(x) 在为这个区间内的增函数;如果在 0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内 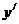 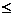 0,那么函数y=f(x) 在为这个区间内的减函数 0,那么函数y=f(x) 在为这个区间内的减函数  2、用导数求函数单调区间的步骤: ①求函数f(x)的导数f′(x). ②令f′(x) 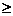 0解不等式,得x的范围就是递增区间. 0解不等式,得x的范围就是递增区间.③令f′(x) 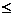 0解不等式,得x的范围,就是递减区间. 0解不等式,得x的范围,就是递减区间.3、例题解析: 例1确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函 数. 解:f′(x)=(x2-2x+4)′=2x-2. 令2x-2>0,解得x>1. ∴当x∈(1,+∞)时,f′(x)>0,f(x)是增函数. 令2x-2<0,解得x<1. ∴当x∈(-∞,1)时,f′(x)<0,f(x)是减函数. 例2确定函数f(x)=2x3-6x2+7在哪个区间内是增函数,哪个区间内是减 函数. 解:f′(x)=(2x3-6x2+7)′=6x2-12x 令6x2-12x>0,解得x>2或x<0 ∴当x∈(-∞,0)时,f′(x)>0,f(x)是增函数. 当x∈(2,+∞)时,f′(x)>0,f(x)是增函数. 令6x2-12x<0,解得0<x<2. ∴当x∈(0,2)时,f′(x)<0,f(x)是减函数. 例3证明函数f(x)= 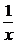 在(0,+∞)上是减函数. 在(0,+∞)上是减函数.证法一:(用以前学的方法证)任取两个数x1,x2∈(0,+∞)设x1<x2. f(x1)-f(x2)=  ∵x1>0,x2>0,∴x1x2>0 ∵x1>0,x2>0,∴x1x2>0∵x1<x2,∴x2-x1>0, ∴  >0 >0∴f(x1)-f(x2)>0,即f(x1)>f(x2) ∴f(x)= 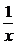 在(0,+∞)上是减函数. 在(0,+∞)上是减函数.证法二:(用导数方法证) ∵f′(x)=( 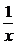 )′=(-1)·x-2=- )′=(-1)·x-2=- ,x>0, ,x>0,∴x2>0,∴-  <0.
∴f′(x)<0,∴f(x)= <0.
∴f′(x)<0,∴f(x)=  在(0,+∞)上是减函数. 在(0,+∞)上是减函数.例4求函数y=x2(1-x)3的单调区间. 解:y′=[x2(1-x)3]′=2x(1-x)3+x2·3(1-x)2·(-1) =x(1-x)2[2(1-x)-3x]=x(1-x)2·(2-5x) 令x(1-x)2(2-5x)>0,解得0<x< 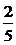 . . ∴y=x2(1-x)3的单调增区间 是(0, 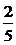 ) 令x(1-x)2(2-5x)<0,解得x<0或x> ) 令x(1-x)2(2-5x)<0,解得x<0或x>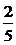 且x≠1. 且x≠1.∵ 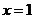 为拐点,∴y=x2(1-x)3的单调减区间是(-∞,0),( 为拐点,∴y=x2(1-x)3的单调减区间是(-∞,0),(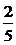 ,+∞) ,+∞)例5.求  的单调递增区间 的单调递增区间解:由函数的定义域可知,  即 即 又  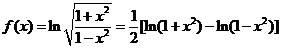 所以  令 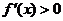 ,得 ,得  或 或 综上所述,  的单调递增区间为(0,1) 的单调递增区间为(0,1)课堂巩固: 1.函数 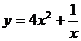 的单调递增区间是( ) 的单调递增区间是( )A  B B 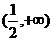 C C  D D  2.已知函数  ,则它的单调递减区间是( ) ,则它的单调递减区间是( )A.  B. B. C. C.  D. D. 及 及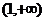 3. 函数   的单调递增区间是__________________. 的单调递增区间是__________________.4.当  时,
时, 在 在 上是减函数. 上是减函数.归纳反思: 合作探究: 1.求函数  的单调区间 的单调区间2.已知函数 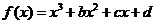 的图象过点 的图象过点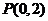 ,且在点 ,且在点 处的切线方程为 处的切线方程为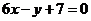 。 。(1)求函数  的解析式;(2)求函数 的解析式;(2)求函数 的单调区间。 的单调区间。 |
教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com