
1下列说法正确的是--------------------------------------------( )
A、 三角形的角平分线是射线。 B、三角形三条高都在三角形内。
C、 三角形的三条角平分线有可能在三角形内,也可能在三角形外。
D、三角形三条中线相交于一点。
2、在Rt△中,两个锐角关系是-------------------------------------------( )
A、互余 B、互补 C、相等 D、以上都不对
2、如图,在△ABC中,∠A=800,∠AB C和∠ACB的外角平分
C和∠ACB的外角平分
 线相交于点D,那么∠BDC= 。
线相交于点D,那么∠BDC= 。
答案1.C 2.500
考查目标二、三角形三边关系
例1长为2,3,5的线段,分别延伸相同长度的线段后,能否组成三角形?若能,它能构成直角三角形吗?为什么?
解题思路:可以,设延伸部分为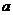 ,则长为
,则长为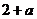 ,
,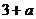 ,
,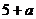 的三条线段中,
的三条线段中,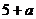 最长, ∵
最长, ∵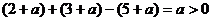
∴只要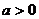 ,长为
,长为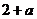 ,
,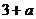 ,
,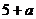 的三条线段可以组成三角形
的三条线段可以组成三角形
设长为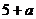 的线段所对的角为
的线段所对的角为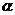 ,则
,则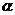 为△ABC的最大角
为△ABC的最大角
又由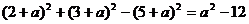
当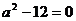 ,即
,即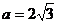 时,△ABC为直角三角形。
时,△ABC为直角三角形。
例2.(2009年温州)下列长度的三条线段能组成三角形的是( )
A.1cm, 2cm, 3.5cm B.4cm, 5cm, 9cm
C.5cm,8cm, 15cm D.6cm,8cm, 9cm
解题思路:三角形任意两边之和大于第三边 答案:D
练习:已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.4cm B.5cm C.6cm D.13cm
答案:C
考查目标三、三角形全等
例1.(2009年浙江省绍兴市)如图,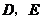 分别为
分别为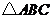 的
的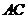 ,
,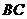 边的中点,将此三角形沿
边的中点,将此三角形沿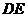 折叠,使点
折叠,使点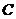 落在
落在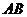 边上的点
边上的点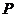 处.若
处.若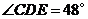 ,则
,则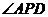 等于( )
等于( )
A.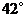 B.
B.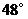 C .
C .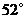 D.
D.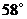

解题思路:折叠前后的两个三角形全等,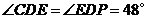 ,CD=DP=AD,再利用三角形中位线定理,答案B
,CD=DP=AD,再利用三角形中位线定理,答案B
 例2、(2009陕西省太原市)如图,
例2、(2009陕西省太原市)如图,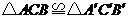 ,
,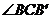 =30°,则
=30°,则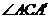 的度数为( )
的度数为( )
A.20° B.30° C.35° D.40°
解题思路: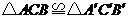 ,
,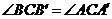 选B
选B
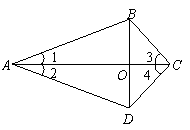 例3(2008年苏州)如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
例3(2008年苏州)如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;(2)BO=DO.
解题思路:
证明:(1)在△ABC和△ADC中
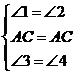
∴△ABC≌△ADC.
(2)∵△ABC≌△ADC,∴AB=AD.又∵∠1=∠2,∴BO=DO.
练习。如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.
(1)给出下列四个条件:
①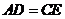 ②
②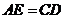 ③
③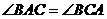 ④
④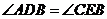
请你从中选出一个能使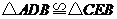 的条件,并给出证明;
的条件,并给出证明;
你选出的条件是 .
证明:
(2)在(1)中所给出的条件中,能使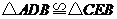 的还有哪些?
的还有哪些?
直接在题后横线上写出满足题意的条件序号: .
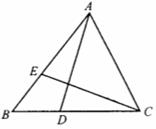
答案:第(1)题添加条件②,③,④中任一个即可,以添加②为例说明.
(1)②证明:∵AE=CD,BE=BD,∴AB=CB,又∠ABD=∠CBE,BE=BD
∴△ADB≌△CEB
(2)③④
过关测试
例7.如图,将两根钢条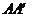 ,
,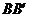 的中点O连在一起,使
的中点O连在一起,使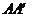 ,
,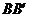 可以绕着点0自由转动,就做成了一个测量工件,则
可以绕着点0自由转动,就做成了一个测量工件,则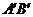 的长等于内槽宽AB,那么判定
的长等于内槽宽AB,那么判定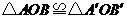 的理由是( )
的理由是( )
A. 边角边 B.角边角 C.边边边 D.角角边
解题思路::新的数学课程标准加强了数学知识的实践与综合应用,从各地的中考应用题可以看出,它已不再局限于传统而古老的列方程(组)解应用题这类题目,而是呈现了建模方式多元化的新特点,几何应用题就是其中之一.本题利用全等三角形来解决实际中的工件的测量问题,其理论依据是“边角边”,故答案为A.
最新考题
三角形是平面几何的重要知识,是历年中考的主要内容之一,主要考查三角形的性质和概念、三角形的内角和定理、三边关系定理、三角形全等的性质与判定、三角形中位线定理以及特殊三角形(等腰三角形、直角三角形)的性质与判定等。
考题以选择为主要考查形式,也将三角形与四边形、圆等知识组成综合性题目进行考查,
而三角形的运动、折叠、拼接形成新数学问题也逐渐增加。
考查目标一、三角形的有关性质
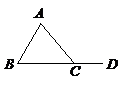 例1.(2009年济宁市)如图,△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于
例1.(2009年济宁市)如图,△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于
A. 100° B. 120° C. 130° D. 150°
解题思路: 运用三角形外角的性质,答案C
 例2.(2009年义乌)如图,在
例2.(2009年义乌)如图,在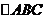 中,
中,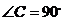 ,EF//AB,
,EF//AB,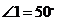 ,则
,则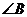 的度数为( )
的度数为( )
A.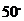 B.
B. 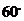 C.
C.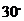 D.
D. 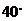
解题思路: 运用三角形内角和定理,答案D
例3(2009年湖北十堰市)下列命题中,错误的是( ).
A.三角形两边之和大于第三边
B.三角形的外角和等于360°
C.三角形的一条中线能将三角形面积分成相等的两部分
D.等边三角形既是轴对称图形,又是中心对称图形
解题思路:等边三角形不是中心对称图形,答案D
练习
1、等腰三角形一腰上的中线分周长为15和12两部分,则此三角形底边之长为( )
A、7
B、11
C、7或11
 D、不能确定
D、不能确定
例6 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
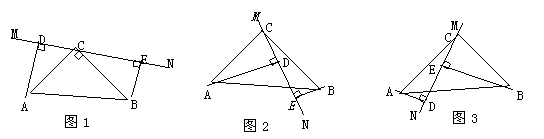 (3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
证明:(1) ① ∵∠ACD=∠ACB=90°,∴∠CAD+∠ACD=90° ,∴∠BCE+∠ACD=90°,∴∠CAD=∠BCE,
∵AC=BC,∴△ADC≌△CEB.
②∵△ADC≌△CEB,∴CE=AD,CD=BE,∴DE=CE+CD=AD+BE.
(2)∵∠ADC=∠CEB=∠ACB=90°, ∴∠ACD=∠CBE ,又∵AC=BC,∴△ACD≌△CBE,
∴∠ACD=∠CBE ,又∵AC=BC,∴△ACD≌△CBE,
∴CE=AD,CD=B E,∴DE=CE-CD=AD-BE.
E,∴DE=CE-CD=AD-BE.
(3)当MN旋转到图3的位置时,AD,DE,BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等).
∵∠ADC=∠CEB=∠ACB=90°,∴∠ACD=∠CBE,又∵AC=BC,∴△ACD≌△CBE,
∴AD=CE,CD=BE,∴DE=CD-CE=BE-AD.
评注:本题以直线MN绕点C旋转过程中与△ABC的不同的位置关系为背景设置的三个小题,第(1)(2)小题为证明题,第(3)小题为探索性问题,考查同学们从具体、特殊的情形出发去探究运动变化过程中的规律的能力,试题的设计层层递进,为发现规律、证明结论设计了可借鉴的过程,通过前面问题解决过程中所提供的思想方法,去解决类似相关问题,考查了同学们的后续学习的能力.
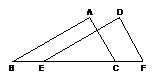 例5.如图,在△ABC和△DEF中,D,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.
例5.如图,在△ABC和△DEF中,D,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
已知:
求证:
证明:
解题思路:题中给出的四个等量关系,以其中三个为条件,另一个作为结论,总共可组成的命题(不论真假)有:①②③ ④ ①②④
④ ①②④ ③ ①③④
③ ①③④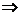 ② ②③④
② ②③④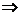 ① 共4个命题,其中真命题有2个,①②④
① 共4个命题,其中真命题有2个,①②④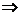 ③或②③④
③或②③④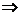 ①,选择其中一个,不难完成题目的解答.
①,选择其中一个,不难完成题目的解答.
解:如①②④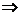 ③
③
证明:∵BE=CF ∴BC=EF 又∵AB=DE, AC=DF
∴△BAC≌△DEF(SSS)
∴∠ABC=∠DEF.
例4.如图,已知CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点O,
且AO平分∠BAC,那么图中全等三角形共有 对.
解题思路:在△ADO与△AEO,根据条件:CD⊥AB,BE⊥AC,AO平分∠BAC及隐含的条件AO=AO(公共边),得到△ADO≌△AEO(AAS);从而得到AD=AE,故Rt△ADC≌Rt△AEB(HL);进一步可推得△ABO≌△ACO(SAS),△BDO≌△CEO(AAS),因此,图中全等三角形共有4对 .
.
例3.如图.∠E=∠F=90°,∠B=∠C.AE=AF,给出下列结论:
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.
其中正确的结论是 .
(注:将你认为正确的结论都填上.)
解题思路:根据已知“∠E=∠F=90°,∠B=∠C.AE=AF”可得△ABE≌△ACF,因此有∠EAB=∠FAC,BE =CF,AC=AB,所以①、②正确;因为∠CAB=∠BAC,∠B=∠C ,AC=AB,所以△ACN≌△ABM,故③也正确;根据条件,无法推出CD=DN,故④不正确.所以,正确的结论是①、②、③.
=CF,AC=AB,所以①、②正确;因为∠CAB=∠BAC,∠B=∠C ,AC=AB,所以△ACN≌△ABM,故③也正确;根据条件,无法推出CD=DN,故④不正确.所以,正确的结论是①、②、③.
评注:将多项选择以填空题的形式出现,是近几年出现的新题型,因答案的不唯一,加大了问题的难度,我们只有对所给的选项一一排查,才能得到正确的答案.
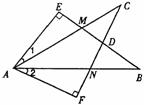
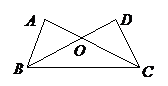 例2 如图所示,在△ABC和△DCB中,AB=DC,要使△ABO≌△DCO,请你补充条件_____________(只要填写一个你认为合适的条件).
例2 如图所示,在△ABC和△DCB中,AB=DC,要使△ABO≌△DCO,请你补充条件_____________(只要填写一个你认为合适的条件).
解题思路:由AB=DC以及图形隐含的对顶角相等:∠AOB=∠DOC可知,要使△ABO≌△DCO,根据(AAS)识别法,直接可补充∠A=∠D或∠ABO=∠DCO.间接可补充:AC=DB.
 评注:本题是一道结论开放性试题,由于全等三角形的识别方法有(SSS)(SAS)(ASA)(AAS)和直角三角形的(HL)识别法,因此,这类题目具有答案不唯一的特点.在添加条件时,要结合图形,挖掘隐含的公共边、公共角、对顶角等条件.
评注:本题是一道结论开放性试题,由于全等三角形的识别方法有(SSS)(SAS)(ASA)(AAS)和直角三角形的(HL)识别法,因此,这类题目具有答案不唯一的特点.在添加条件时,要结合图形,挖掘隐含的公共边、公共角、对顶角等条件.
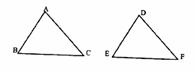 例1 如图,在△ABC与△DEF中,给出以下六个条件中(1)AB=DE(2)BC=EF(3)AC=DF (4)∠A=∠D(5)∠B=∠E(6)∠C=∠F,以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
例1 如图,在△ABC与△DEF中,给出以下六个条件中(1)AB=DE(2)BC=EF(3)AC=DF (4)∠A=∠D(5)∠B=∠E(6)∠C=∠F,以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3)
C.(4)(6)(1) D.(2)(3)(4)
解题思路:根据全等三角形的识别方法及给出的四个答案,一一加以辨别,因为用(SAS)识别法中,两边对应相等的话,一定要夹角对应相等,所以答案(D)不能判断△ABC与△DEF全等.
38. own 拥有,自己的 on one's own = by oneself
of one's own …自己所有的 I own a shop.
|
|
版权所有:()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com