
34.已知函数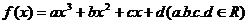 ,且函数
,且函数 的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
(1)
求 的解析式;
的解析式;
(2)
是否存在区间[a,b],使得函数g(x)的定义域和值域均为[a,b],且解析式与 的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
解:(1)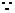
 的图像关于原点对称,
的图像关于原点对称,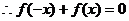 恒成立,即
恒成立,即 恒成立,
恒成立,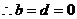 。
。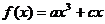 ,
,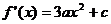
又 的图像在x=3处的切线方程为
的图像在x=3处的切线方程为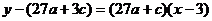 ,
,
即 ,据题意得:
,据题意得: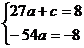 解得:
解得: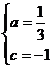 ,
,
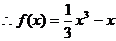
(2)由 得x=0或
得x=0或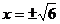 。
。
又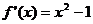 ,由
,由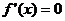 得
得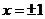 ,且当
,且当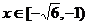 或
或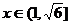 时,
时,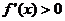 ,当
,当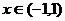 时
时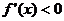 。
。
所以,函数 在
在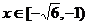 和
和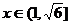 上递增,在
上递增,在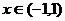 上递减。
上递减。
于是,函数在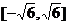 上的极大值和极小值分别为
上的极大值和极小值分别为
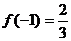 ,
,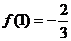 而
而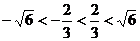 ,
,
故存在这样的区间[a,b],其中满足条件的一个区间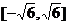
33.曲线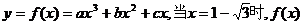 有极小值,当
有极小值,当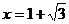 处有极大值,且在x=1处切线的斜率为
处有极大值,且在x=1处切线的斜率为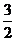 .
.
(1)求 ;
;
(2)曲线上是否存在一点P,使得y= 的图象关于点P中心对称?若存在,请求出点P坐标,并给出证明;若不存在,请说明理由.
的图象关于点P中心对称?若存在,请求出点P坐标,并给出证明;若不存在,请说明理由.
解:f′(x)=3ax2+2bx+c ∵当x=1± 时 f(x)有极小值及极大值
时 f(x)有极小值及极大值
∴f′(1± )=0 即1±
)=0 即1± 为3ax2+2bx+c=0两根
为3ax2+2bx+c=0两根
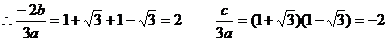
∴b=-3a , c=-6a
又∵f(x)在x=1处切线的斜率为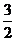
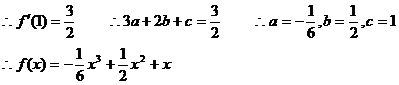
(2)假设存在P(x0, y0),使得f(x)的图象关于P中心对称,
则f(x0+x)+f(x0-x)=2y0
即-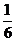 (x0+x)3+
(x0+x)3+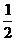 (x0+x)2+x0+x-
(x0+x)2+x0+x-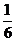 (x0-x)3+
(x0-x)3+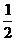 (x0-x)2+x0-x=2y0
(x0-x)2+x0-x=2y0
化解得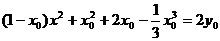
∵对于任意x∈R等式都成立
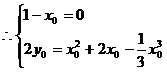
∴x0=1, y0=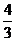 .易知P(1,
.易知P(1,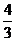 )在曲线y=f(x)上.
)在曲线y=f(x)上.
∴曲线上存在P(1,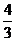 )使得f(x)的图象关于中心对称
)使得f(x)的图象关于中心对称
32. 如图,平面PAD
如图,平面PAD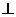 平面ABCD,
平面ABCD, PAD是正三角形,
PAD是正三角形,
ABCD是矩形,M是AB的中点,PC与平面ABCD成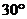 角。
角。
(1)
求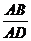 的值;
的值;
(2) 求二面角P-MC-D的大小;
(3) 当AD的长为多少时,点D到平面PMC的距离为2。
解:(1)取AD中点H,则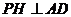 ,
,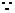 面PAD
面PAD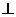 平面ABCD,
平面ABCD,
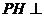 面ABCD,
面ABCD, PC与面ABCD所成的角为
PC与面ABCD所成的角为 。
。
设AD=a,则 ,
, ,
,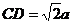

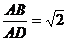 。
。
(2)连结HM,由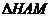 ∽
∽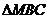 可得:
可得: 。
。
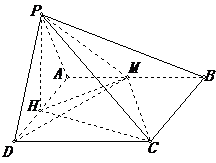
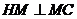 ,由三垂线定理得
,由三垂线定理得 ,
,

 是二面角P-MC-D的平面角。
是二面角P-MC-D的平面角。
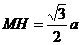 ,
,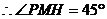 。
。
二面角P-MC-D的平面角为
由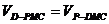 可得:AD=
可得:AD=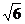 。
。
31.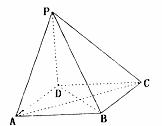 已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
(Ⅰ)求PC与平面PBD所成的角;
(Ⅱ)求点D到平面PAC的距离;
(Ⅲ)在线段PB上是否存在一点E,使PC⊥平面ADE?
若存在,确定E点的位置,若不存在,说明理由.
解: (Ⅰ)设AC与BD相交于点O,连接PO。
∵ABCD是正方形,∴AC⊥BD。
又∵PD⊥平面ABCD,∴PD⊥AC。
∵BD∩PD=D, ∴AC⊥平面PBD。
∴∠CPO为PC与平面PBD所成的角。
∵PD=AD=2,则OC= ,PC=2
,PC=2 。
。
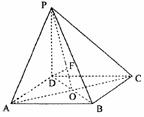 在Rt△POC中,∠POC=90°,
在Rt△POC中,∠POC=90°,
∴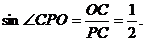
∴PC与平面PBD所成的角为30°
(Ⅱ)过D做DF⊥PO于F,∵AC⊥平面PBD,
DF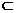 平面PBD, ∴AC⊥DF。
平面PBD, ∴AC⊥DF。
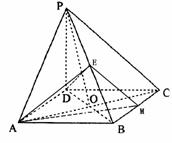 又∵PO∩AC=O,
∴DF⊥平面PAC。
又∵PO∩AC=O,
∴DF⊥平面PAC。
在Rt△PDO中,∠PDO=90°,
∴PO·DF=PD·DO。 ∴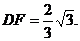
(Ⅲ)假设存在E点,使PC⊥平面ADE.
过E在平面PBC内做EM∥PC交BC于点M,
连接AE、AM.
由AD⊥平面PDC可得AD⊥PC. ∵PC∥EM,∴AD⊥EM.
要使PC⊥平面ADE,即使EM⊥平面ADE. 即使EM⊥AE.
设BM= ,则EM=
,则EM=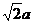 ,EB=
,EB=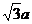 . 在△AEB中由余弦定理得AE2=4+3
. 在△AEB中由余弦定理得AE2=4+3 -4
-4
在Rt△ABM中,∠ABM=90°. ∴AM2=4+ .
.
∵EM⊥AE,∴4+ =4+3
=4+3 -4
-4 +2
+2 . ∴
. ∴ -
- =0. ∵
=0. ∵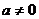 ,∴
,∴ =1.
=1.
∴E为PB的中点,即E为PB的中点时,PC⊥平面ADE.
30.某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管与其费用为平均每天3元,购买面粉每次支付运费900元。
(1) 求该厂多少购买一次面粉才能使平均每天支付的总费用最小;
(2) 若提供面粉的公司规定,当一次购买面粉不少210吨时其价格可享受九折惠(即原价的90%)。问该厂是否考虑利用此优惠条件,请说明理由。
解(1)设该厂应隔x天购买一次面粉,其购买量为6x吨,则面粉的保管与其它费用
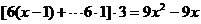 ,平均每天支出的费用为
,平均每天支出的费用为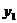 ,则
,则


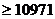

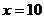
即每隔10天购买一次才能使平均每天支付的总费用最小。
(2)若厂家利用此优惠条件,则至少35天购买一次面粉,设该厂利用此优惠条件,每隔x天(x ) 购买一次面粉,平均每天支出的费用为
) 购买一次面粉,平均每天支出的费用为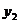 。
。

利用单调性可证
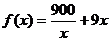 在
在 上递增。
上递增。
 时
时 取得最小值,即
取得最小值,即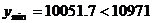 ,
,
 该厂应接受此优惠条件。
该厂应接受此优惠条件。
29. 某人抛掷一枚硬币,出现正反的概率都是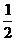 ,构造数列
,构造数列 ,使得
,使得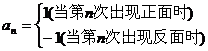 ,记
,记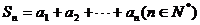 。
。
(1)
求 的概率;
的概率;
(2)
若前两次均出现正面,求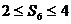 的概率。
的概率。
解:(1) ,需4次中有3次正面1次反面,设其概率为
,需4次中有3次正面1次反面,设其概率为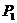
则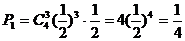
(2)6次中前两次均出现正面,要使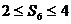 ,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为
,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为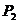 。
。
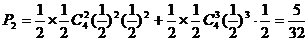
28.已知
且 (1)求
(1)求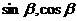 ; (2)求
; (2)求
解:(1)由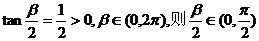



(2)由
则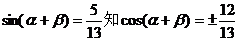
由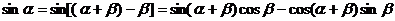
在 时,
时,
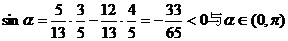 矛盾,故舍去.
矛盾,故舍去.
在 可取. 因此
可取. 因此
27. 若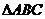 中,a,b,c分别是
中,a,b,c分别是 的对边,且
的对边,且 ,
,
(1)
求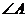 ;
;
(2)
若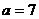 ,
, 的面积为
的面积为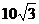 ,求b+c的值。
,求b+c的值。
解:(1)由 得:
得: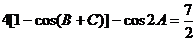 ,
,
可得: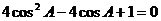 ,
, ,
,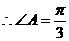 。
。
(2)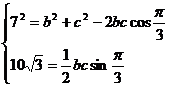
 ,
,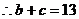 。
。
26. 如下图,它满足:
如下图,它满足:
(1) 第n行首尾两数均为n ;
(2)表中的递推关系类似杨辉三角.
则第n行(n≥2)第2个数是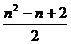 。
。
25.有一组数据: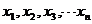
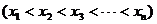 的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数
的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数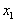 关于
关于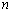 的表达式是
的表达式是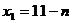 ,第
,第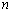 个数
个数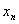 关于
关于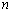 的表达式是
的表达式是 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com