
2、集中和分散相结合,提高重要实验的复现率
化学实验专题的复习一般都安排在最后一个部分,而化学实验知识又与其它化学知识体系不可分割。在复习过程中对化学实验内容必须注意集中和分散相结合。“集中”,就是集中复习实验的基本操作和技能,集中复习一些综合性的实验专题,集中归纳总结实验知识。而“分散”则是指一些性质实验、制法实验、验证或探索性实验等应分散到元素化合物、有机物、使用注意事项:
①加热时应放置在石棉网上,使受热均匀。
②溶解物质用玻璃棒搅拌时,不能触及杯壁或杯底。
1、营造民主和谐教学环境,发挥学生的主体作用
由于化学实验知识具有内容多而散的特点,在专题复习中更应该注重学生的参与活动,切实发挥学生的主体作用。在复习教学中要进一步创设环境,让学生多动手多动脑,并师生之间和同学之间的进行多渠道多层次的交流与沟通。在复习中可以通过布置复习的知识点具体目标要求,促进学生对有关知识进行归纳和总结。通过实验室进行化学实验的展览和开放实验室活动,使学生进一步直观地复习化学实验知识,并提高学生的动手能力和创新意识。
3.运用所学知识和技能进行实验设计或处理
近年来,实验题中新情境试题不断增多,这类试题的特点是将基本的实验操作设计置于新的情境中(主要是中学课本没有的新反应或新装置或是能使中学生理解的最新科技知识、简化的改进的装置等),结合学生原有的知识和能力,来进行仪器组装、现象描述、数据分析、考虑安全和防污等,用来考查考生自学能力、思维能力、分析综合及评价的能力。由于这类实验试题情境新颖、设问巧妙、铺垫得当、知识新、思维量大、所以区分度很好,能确实将一些基础扎实、自学能力强、思维敏捷、心理素质好的考生选拨出来。所以,新情境实验试题将是今后实验试题的命题方向。
由以上分析不难看出,尽管化学实验部分涉及到的知识和能力点是分散的,但高考试题中实验考查的内容和形式是较为稳定的,这给实验复习中突出重点提供了可能。实验复习根据考纲和高考试题的几个特点方面,设计化学实验专题加以重点复习,就会起到事半功倍的效果。
复习教学方法设计
化学实验的复习是整个化学总复习中一个非常重要的环节,它不但可以巩固和强化有关化学实验知识和能力,也能对元素化学物知识、化学基本理论和化学计算内容的掌握起到促进和深化作用。由于化学实验部分的内容多且在课本中十分的分散,在实验复习教学中,必须有的放矢、突出重点。这个“的”就是“考试说明”所规定的考查内容,而重点就是历年来高考试题中所反映的考试内容。在进行实验部分的专题复习中应该注意以下几点:
根据近年来化学高考试题中有关化学实验内容的题目分析,下列内容是化学实验部分考查的重点:
l.实验基本操作和技能
这类试题的特点通常是给出限定的仪器、药品和一些操作步骤,要求正确完成某项实验操作,既有常见仪器的使用方法,又有基本操作的正误辨别,着重考查考生对中学化学实验基本操作技能掌握的情况,题目的难度不高,但并不容易得满分。
2.正确运用实验原理和正确认识实验装置
这类试题通常是给出限定的实验装置、反应条件、实验现象和有关数据,要求考生根据实验原理及试题中所给予的信息,结合元素化合物知识,选用仪器药品,正确认识、选择装置,说明装置中某些仪器的作用,描述实验现象,写有关化方程式,进行数据分析.指出实验中必须注意的某些问题等等,主要考查考生的观察能力与分析综合及评价的能力。这类题目具有一定的综合性,具有较大的区分度。
22.已知椭圆C1: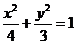 ,抛物线C2:
,抛物线C2: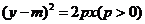 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(1)当AB⊥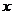 轴时,求
轴时,求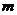 、
、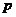 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(2)是否存在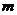 、
、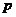 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的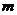 、
、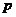 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
2007-2008学年度南昌市高三第一轮复习训练题
21. 已知椭圆 ,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线
,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线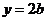 于点N,且
于点N,且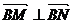 .
.
(1)求椭圆的离心率;
(2)若斜率为1的直线l交椭圆于P、Q两点,求证: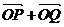 与向量
与向量 =(-3,1)共线(其中O为坐标原点)
=(-3,1)共线(其中O为坐标原点)
20.(理)已知动点M到点F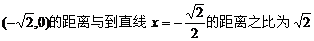 .
.
(1)求动点M的轨迹C的方程;
(2)若过点E(0,1)的直线与曲线C在y轴左侧交于不同的两点A、B,点P(-2,0)满足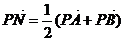 ,求直线PN在y轴上的截距d的取值范围..
,求直线PN在y轴上的截距d的取值范围..
(文)直线l: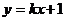 与曲线
与曲线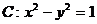 的左支交于不同的两点A、B,直线m过点P(-2,0)和AB的中点M,求m在y轴上截距b的取值范围.
的左支交于不同的两点A、B,直线m过点P(-2,0)和AB的中点M,求m在y轴上截距b的取值范围.
19. 已知椭圆
已知椭圆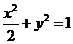 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(1)求过点O、F,并且与椭圆的左准线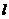 相切的圆的方程;
相切的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,
线段AB的垂直平分线与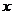 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
17. 过抛物线
过抛物线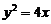 的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2 + 2y2
= 2相交,求k的取值范围.
的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2 + 2y2
= 2相交,求k的取值范围.


 18.若点P在椭圆
18.若点P在椭圆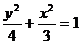 上,设
上,设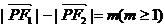 ,(1)试用m表示
,(1)试用m表示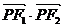 ;
;
(2)在(1)的条件下,求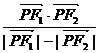 的最大值和最小值
的最大值和最小值
16. 已知抛物线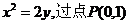 的直线与抛物线相交于
的直线与抛物线相交于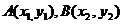 两点,则
两点,则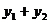 的最小值是___________
的最小值是___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com