
31.(2008桂林市)
已知:△ABC为等边三角形,D为AC上任意一点,连结BD
(1)在BD左下方,以BD为一边作等边三角形BDE(尺规作图,保留作图痕迹,不写作法)(2)连结AE,求证:CD=AE

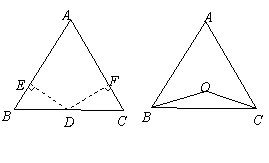
30.(2008湖北宜昌市).如图,在△ABC和△ABD中,BC=BD,设点E是BC的中点,点F是BD的中点.
(1)请你在图中作出点E和点F;(要求用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接AE、AF.若∠ABC=∠ABD,请你证明△ABE≌△ABF.
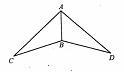
29.(2008山东济宁)如图,在 中,
中,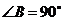 ,
,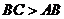 .
.
(1)在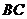 边上找一点
边上找一点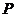 ,使
,使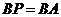 ,分别过点
,分别过点 作
作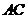 的垂线
的垂线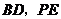 ,垂足为
,垂足为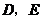 .
.
(2)在四条线段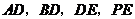 中,某些线段之间存在一定的数量关系.请你写出一个等式表示这个数量关系(等式中含有其中的2条或3条线段),并说明等式成立的理由.
中,某些线段之间存在一定的数量关系.请你写出一个等式表示这个数量关系(等式中含有其中的2条或3条线段),并说明等式成立的理由.
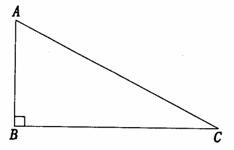
28.(2008福建省泉州市)已知:如图,E、C两点在线段BF上,BE=CF,AB=DE,
AC=DF,求证: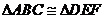

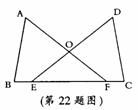
27.(2008黑龙江哈尔滨)已知:如图,B、E、F、C四点在同一条直线上,AB=DC,BE=CF,∠B=∠C.
求证:OA=OD.
26.(2008四川达州市)(6分)含 角的直角三角板
角的直角三角板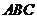 (
(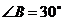 )绕直角顶点
)绕直角顶点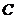 沿逆时针方向旋转角
沿逆时针方向旋转角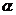 (
(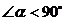 ),再沿
),再沿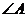 的对边翻折得到
的对边翻折得到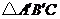 ,
,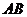 与
与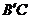 交于点
交于点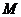 ,
,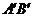 与
与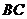 交于点
交于点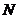 ,
,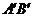 与
与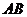 相交于点
相交于点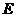 .
.
(1)求证: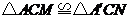 .
.
(2)当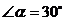 时,找出
时,找出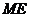 与
与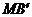 的数量关系,并加以说明.
的数量关系,并加以说明.
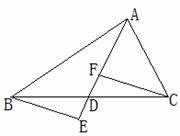
25.(2008浙江湖州) 如图,在△ABC中,D是BC边的中点,F、E分别是AD及延长线上的点,
CF∥BE,
(1)求证:△BDE≌△CDF
(2)请连结BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由。
24.(2008山西太原)将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片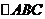 和
和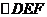 。将这两张三角形胶片的顶点B与顶点E重合,把
。将这两张三角形胶片的顶点B与顶点E重合,把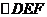 绕点B顺时针方向旋转,这时AC与DF相交于点O。
绕点B顺时针方向旋转,这时AC与DF相交于点O。

(1)当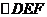 旋转至如图②位置,点B(E),C,D在同一直线上时,
旋转至如图②位置,点B(E),C,D在同一直线上时,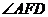 与
与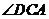 的数量关系是
。
的数量关系是
。
(2)当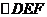 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由。
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由。
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明。
23.(2008泰安) 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,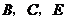 在同一条直线上,连结
在同一条直线上,连结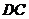 .
.


(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:
22.(2008安徽)已知:点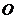 到
到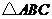 的两边
的两边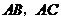 所在直线的距离相等,且
所在直线的距离相等,且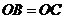 .
.
(1)如图1,若点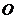 在边
在边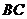 上,求证:
上,求证: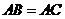 ;
;
(2)如图2,若点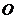 在
在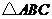 的内部,求证:
的内部,求证: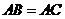 ;
;
(3)若点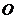 在
在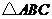 的外部,
的外部,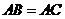 成立吗?请画图表示.
成立吗?请画图表示.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com