
1.(1)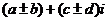
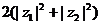
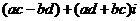
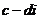
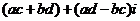
(2)交换律 分配律 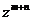
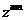
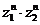
12. 解:(Ⅰ)由题设,|ω|=|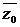 ·
·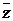 |=|z0||z|=2|z|,∴|z0|=2,
|=|z0||z|=2|z|,∴|z0|=2,
于是由1+m2=4,且m>0,得m= ,
,
因此由x′+y′i=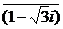 ·
·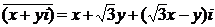 ,
,
得关系式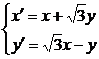
(Ⅱ)设点P(x,y)在直线y=x+1上,则其经变换后的点Q(x′,y′)满足
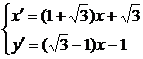 ,消去x,得y′=(2-
,消去x,得y′=(2- )x′-2
)x′-2 +2,
+2,
故点Q的轨迹方程为y=(2- )x-2
)x-2 +2.
+2.
(Ⅲ)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,∴所求直线可设为y=kx+b(k≠0).
解:∵该直线上的任一点P(x,y),其经变换后得到的点Q(x+ y,
y, x-y)仍在该直线上,∴
x-y)仍在该直线上,∴ x-y=k(x+
x-y=k(x+ y)+b,即-(
y)+b,即-( k+1)y=(k-
k+1)y=(k- )x+b,
)x+b,
当b≠0时,方程组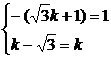 无解,故这样的直线不存在.
无解,故这样的直线不存在.
当b=0,由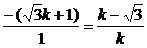 ,得
,得 k2+2k
k2+2k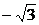 =0,解得k=
=0,解得k=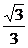 或k=
或k=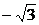 ,
,
故这样的直线存在,其方程为y=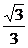 x或y=
x或y=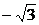 x.
x.
第二讲 复数的运算
[知识梳理]
[知识盘点]
11. 解:设z=a+bi(a,b∈R),则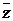 =a-bi,代入4z+2
=a-bi,代入4z+2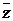 =3
=3 +i
+i
得4(a+bi)+2(a-bi)=3 +i.∴
+i.∴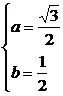 .∴z=
.∴z=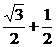 i.
i.
|z-ω|=|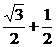 i-(sinθ-icosθ)|
i-(sinθ-icosθ)|
=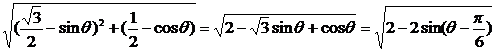
∵-1≤sin(θ- )≤1,∴0≤2-2sin(θ-
)≤1,∴0≤2-2sin(θ- )≤4.∴0≤|z-ω|≤2.
)≤4.∴0≤|z-ω|≤2.
10.解:要使复数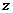 为纯虚数,必须
为纯虚数,必须 且
且 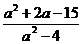
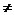 0,
0,
即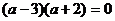 ,解得
,解得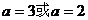
但是,当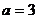 时
时 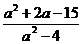 =0此时
=0此时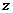 不是纯虚数
不是纯虚数
当 时,
时,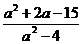 无意义
无意义
所以不存在实数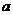 使
使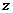 为纯虚数
为纯虚数
1.A 2.C 3.A 4.D 5.C 6.-1 7.椭圆 8.四 9.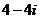
6. 解:(Ⅰ)∵z是方程x2+1=0的根,∴z1=i或z2=-i,不论z1=i或z2=-i,
Mz={i,i2,i3,i4}={i,-1,-i,1},于是P=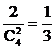 .
.
(Ⅱ)取z=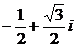 ,则z2=
,则z2=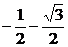 i及z3=1.
i及z3=1.
于是Mz={z,z2,z3}或取z=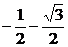 i.(说明:只需写出一个正确答案).
i.(说明:只需写出一个正确答案).
[能力提升]
5.解: (Ⅰ) 由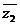 =z1+2i , 两边同时取共轭复数可得: z2=
=z1+2i , 两边同时取共轭复数可得: z2=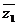 -2i . 代入已知方程得: z1(
-2i . 代入已知方程得: z1(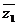 -2i )+ 2i z1-2i(
-2i )+ 2i z1-2i(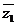 -2i)+1=0. 即|z1|2-2i
-2i)+1=0. 即|z1|2-2i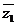 -3=0. 令z1=a+bi , 即可得到 a2+b2-2i(a-bi)-3=0.
-3=0. 令z1=a+bi , 即可得到 a2+b2-2i(a-bi)-3=0.
即 (a2+b2-2b-3)- 2ai =0. 解得a=0, b=3,或a=0, b=-1.
∴z1=3i, z2=-5i, 或z1=-i , z2=-i .
(Ⅱ)由已知得z1=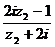 . 又∵|z1|=
. 又∵|z1|=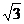 , ∴|
, ∴|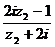 |=
|=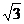 .∴| 2i z2-1|2=3|z2+ 2i|2.
.∴| 2i z2-1|2=3|z2+ 2i|2.
∴(2i z2-1)( -2i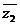 -1)=3(z2+ 2i)(
-1)=3(z2+ 2i)(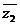 - 2i). 整理得: z2
- 2i). 整理得: z2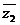 +4i z2-4i
+4i z2-4i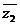 -11=0.
-11=0.
即(z2-4i)( 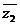 +4i)=27. ∴| z2-4i|2=27, 即| z2-4i|=3
+4i)=27. ∴| z2-4i|2=27, 即| z2-4i|=3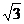 .
.
∴存在常数k=3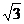 , 使得等式| z2-4i|=k恒成立.
, 使得等式| z2-4i|=k恒成立.
4.解:(Ⅰ)设z=a+bi,a、b∈R,b≠0
则w=a+bi+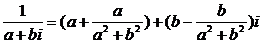
因为w是实数,b≠0,所以a2+b2=1,即|z|=1.于是w=2a,-1<w=2a<2,-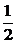 <a<1,
<a<1,
所以z的实部的取值范围是(-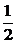 ,1).
,1).
(Ⅱ)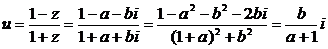 .
.
因为a∈(-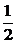 ,1),b≠0,所以u为纯虚数.
,1),b≠0,所以u为纯虚数.
(Ⅲ)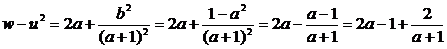
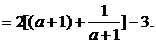 .
.
因为a∈(-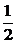 ,1),所以a+1>0,故w-u2≥2·2
,1),所以a+1>0,故w-u2≥2·2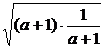 -3=4-3=1.
-3=4-3=1.
当a+1=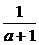 ,即a=0时,w-u2取得最小值1.
,即a=0时,w-u2取得最小值1.
3. 解:设z=x+yi(x、y∈R),∵|z|=5,∴x2+y2=25,
而(3+4i)z=(3+4i)(x+yi)=(3x-4y)+(4x+3y)i,
又∵(3+4i)z在复平面上对应的点在第二、四象限的角平分线上,
∴3x-4y+4x+3y=0,得y=7x,∴x=±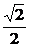 ,y=±
,y=±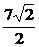
即z=±(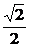 +
+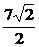 i);
i);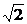 z=±(1+7i).
z=±(1+7i).
当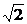 z=1+7i时,有|1+7i-m|=5
z=1+7i时,有|1+7i-m|=5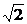 ,
,
即(1-m)2+72=50,得m=0,m=2.
当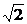 z=-(1+7i)时,同理可得m=0,m=-2.
z=-(1+7i)时,同理可得m=0,m=-2.
2.解:⑴当 ,即x=a或
,即x=a或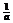 时z为实数;
时z为实数;
⑵当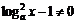 ,即
,即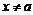 且
且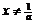 时z为虚数;
时z为虚数;
⑶当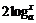 =0且
=0且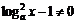 ,即x=1时z为纯虚数
,即x=1时z为纯虚数
⑷当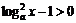 ,即当0<a<1时,0<x<a或x>
,即当0<a<1时,0<x<a或x>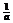 ;或a>1时,x>a或0<x<
;或a>1时,x>a或0<x<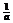 时z在复平面上对应的点在实轴上方;
时z在复平面上对应的点在实轴上方;
⑸当 +
+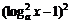 =1即x=1时,|z|=1.
=1即x=1时,|z|=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com