
一个正方形的周长与一个等腰三角形的周长相等,若等腰三角形的两边长为 和 和 ,则这个正方形的对角线长为 ,则这个正方形的对角线长为 |
A.12 B.  C.2  D.6  |
科目:初中数学 来源:不详 题型:单选题
| 2 |
| 2 |
| A.12 | B.
| C.2
| D.6
|
科目:初中数学 来源: 题型:解答题
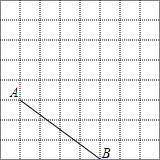 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一条线段AB,点A、B均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一条线段AB,点A、B均与小正方形的顶点重合.科目:初中数学 来源: 题型:
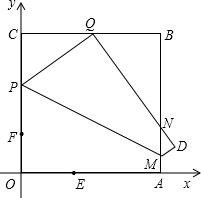
科目:初中数学 来源: 题型:解答题
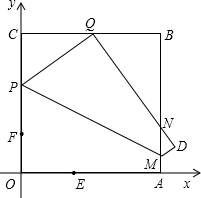
科目:初中数学 来源:2011年河南省郑州市中考数学模拟试卷(2)(解析版) 题型:解答题

科目:初中数学 来源:2011年新疆乌鲁木齐市中考数学押题卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:
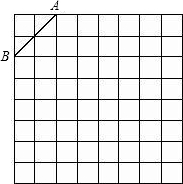 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com