| 以如下的a、b、c为三边长的三角形不是直角三角形的是 |
A.
B.a=1.5,b=2,c=2.5
C.a:b:c=5:12:13
D.a=2k,b=3k,c=4k |
相关习题
科目:初中数学
来源:山东省期中题
题型:单选题
以如下的a、b、c为三边长的三角形不是直角三角形的是
A.
B.a=1.5,b=2,c=2.5
C.a:b:c=5:12:13
D.a=2k,b=3k,c=4k
查看答案和解析>>
科目:初中数学
来源:
题型:
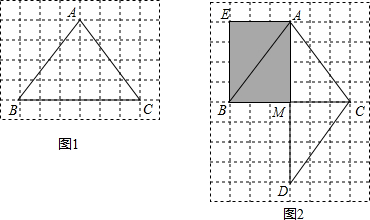
把三角形形状的纸片放在方框纸上,使其每一个顶点都在格点上,如图1所示(方格边长均为1).对这个三角形进剪切、拼接后,可以得到一个平行四边形,如图2中阴影部分所示.
剪切、拼接的方案如下:如图2,取BC的中点M,连AM.剪下△AMC后,沿直线BC翻折,所得图形称为△DMC;再把△DMC沿射线CA方向平移线段CA的长度后,可得到平行四边形AEBM.
我们约定:剪切、拼接 时,纸片的每一部分都要被用到,而且不得用所给纸片以外的纸片.
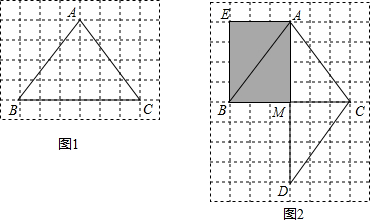
(1)请你采用不同于图2的剪切、拼接方案,也得到一个平行四边形,并说明你的剪切、拼接方案,同时在图3中用阴影表示出你得到的平行四边形;
(2)对这个三角形进行剪切、拼接后,也可以得到一梯形.试在图4中,用阴影表示出你得到的梯形(不必说明剪切、拼接方案,但必须保留作图痕迹).
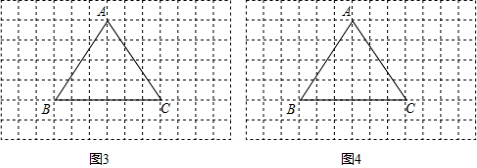
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
把三角形形状的纸片放在方框纸上,使其每一个顶点都在格点上,如图1所示(方格边长均为1).对这个三角形进剪切、拼接后,可以得到一个平行四边形,如图2中阴影部分所示.
剪切、拼接的方案如下:如图2,取BC的中点M,连AM.剪下△AMC后,沿直线BC翻折,所得图形称为△DMC;再把△DMC沿射线CA方向平移线段CA的长度后,可得到平行四边形AEBM.
我们约定:剪切、拼接 时,纸片的每一部分都要被用到,而且不得用所给纸片以外的纸片.
(1)请你采用不同于图2的剪切、拼接方案,也得到一个平行四边形,并说明你的剪切、拼接方案,同时在图3中用阴影表示出你得到的平行四边形;
(2)对这个三角形进行剪切、拼接后,也可以得到一梯形.试在图4中,用阴影表示出你得到的梯形(不必说明剪切、拼接方案,但必须保留作图痕迹).
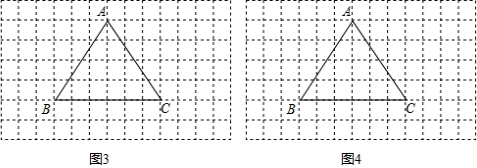
查看答案和解析>>
科目:初中数学
来源:学习周报 数学 华师大八年级版 2009-2010学年 第8期 总第164期 华师大版
题型:044
判断以如下的a、b、c为边长的三角形是不是直角三角形
(1)a=11,b=60,c=61;(2)a= ,b=1,c=
,b=1,c= .
.
查看答案和解析>>
科目:初中数学
来源:
题型:044
试判断以如下的a、b、c为三边长的三角形是不是直角三角形.如果是,那么哪一条边所对的角是直角?
(1)a=25,b=20,c=15;
(2)a=1,b=2,

;
(3)a=40,b=9,c=40;
(4)a:b:c=5:12:13.
查看答案和解析>>
科目:初中数学
来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版
题型:047
|
|
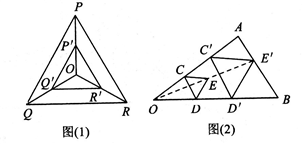
位似三角形
如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位
似中心.利用三角形的位似可以将一个三形缩小或放大.
| (1) |
|
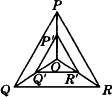
如图,点O是等边三角形PQR的中心,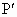 、 、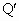 、 、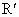 分别是OP、OQ、OR的中点,则△ 分别是OP、OQ、OR的中点,则△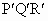 与△PQR是位似三角形.此时,△ 与△PQR是位似三角形.此时,△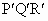 与△PQR的位似比、位似中心分别为 与△PQR的位似比、位似中心分别为
|
| [ ] |
A. |
2;点P
|
B. |
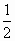 ;点P ;点P
|
C. |
2;点O
|
D. |
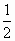 ;点O ;点O
|
|
(2) |
|
|
查看答案和解析>>
科目:初中数学
来源:同步题
题型:解答题
如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,对应边平行,那么这两个三角形也是位似三角形,它们的相似比是位似比,这个点是位似中心,利用三角形的位似可以将一个三角形缩小或放大。
(1)如图(1)所示,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似比、位似中心分别为( )
A.2、点P
B.
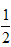
、点P
C.2、点O
D.
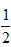
、点O
(2)如图(2)所示,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题。
画法:
①在△ABO内画等边△CDE,使点C在OA上,点D在OB上;
②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E'D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接等边三角形,试说明△C′D′E′是等边三角形。
查看答案和解析>>
科目:初中数学
来源:
题型:
 是等边三角形,D是射线BC上的一个动点(与点B、C不重合),
是等边三角形,D是射线BC上的一个动点(与点B、C不重合), 是以AD为边的等边三角形,过点E作
是以AD为边的等边三角形,过点E作 ,交射线AC于点F,连结BE.
,交射线AC于点F,连结BE.
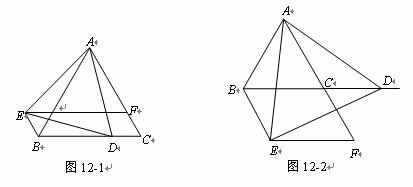
(1)如图 ,当点D在线段BC上运动时。①求证:
,当点D在线段BC上运动时。①求证: ;②探究四边形BCFE是怎样的四边形?并说明理由;
;②探究四边形BCFE是怎样的四边形?并说明理由;
(2)如图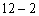 ,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCFE是菱形?并说明理由。
查看答案和解析>>
科目:初中数学
来源:不详
题型:解答题
是等边三角形,D是射线BC上的一个动点(与点B、C不重合),
是以AD为边的等边三角形,过点E作

,交射线AC于点F,连结BE.
(1)如图

,当点D在线段BC上运动时。①求证:

;②探究四边形BCFE是怎样的四边形?并说明理由;

(2)如图

,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCFE是菱形?并说明理由。

查看答案和解析>>
科目:初中数学
来源:数学教研室
题型:044
如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一
个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做
位似中心。利用三角形的位似可以将一个三角形缩小或放大。
(1)选择:如图(1),点O是等边△PQR的中心,P’Q’R’分别是OP、OQ、OR的
中点,则△P’Q’R’与是△PQR是位似三角形,此时,△P’Q’R’与△PQR的位似比,位
似中心分别为
( )
A. 2,点P B. ,点P C. 2,点O D. ,点O
(2)如图(2),用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应的
问题。画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②
连结OE并延长,交AB于点E’,过点E’作E’C’//EC,交OA于点C’,作E’D’//ED,
交OB于点D’;③连结C’D’,则△C’D’E’
查看答案和解析>>



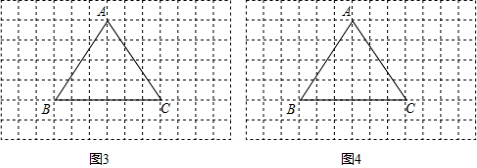

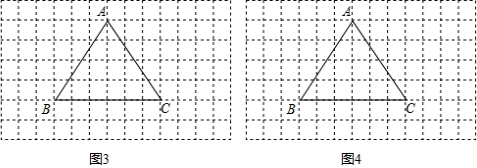
![]() ,b=1,c=
,b=1,c=![]() .
. ;
;
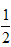 、点P
、点P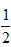 、点O
、点O![]() 是等边三角形,D是射线BC上的一个动点(与点B、C不重合),
是等边三角形,D是射线BC上的一个动点(与点B、C不重合),![]() 是以AD为边的等边三角形,过点E作
是以AD为边的等边三角形,过点E作![]() ,交射线AC于点F,连结BE.
,交射线AC于点F,连结BE.![]() ,当点D在线段BC上运动时。①求证:
,当点D在线段BC上运动时。①求证:![]() ;②探究四边形BCFE是怎样的四边形?并说明理由;
;②探究四边形BCFE是怎样的四边形?并说明理由;![]() ,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
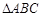 是等边三角形,D是射线BC上的一个动点(与点B、C不重合),
是等边三角形,D是射线BC上的一个动点(与点B、C不重合),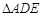 是以AD为边的等边三角形,过点E作
是以AD为边的等边三角形,过点E作 ,交射线AC于点F,连结BE.
,交射线AC于点F,连结BE. ,当点D在线段BC上运动时。①求证:
,当点D在线段BC上运动时。①求证: ;②探究四边形BCFE是怎样的四边形?并说明理由;
;②探究四边形BCFE是怎样的四边形?并说明理由;
 ,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;