
科目:高中数学 来源: 题型:解答题
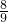 的等比数列的前n项和.
的等比数列的前n项和.科目:高中数学 来源:河西区二模 题型:解答题
| 8 |
| 9 |
科目:高中数学 来源:《数列》2013年高三数学一轮复习单元训练(浙江大学附中)(解析版) 题型:解答题
 的等比数列的前n项和.
的等比数列的前n项和.科目:高中数学 来源:江西省浮梁一中2007届高三数学重组卷二(人教版) 题型:038
已知等差数列{an}的首项为a,公差为b;等比数列{bn}的首项为b,公比为a,其中a,b∈N+,且a1<b1<a2<b2<a3.
(1)求a的值;
(2)若对于任意n∈N+,总存在m∈N+,使am+3=bn,求b的值;
(3)在(2)中,记{cn}是{an}中所有满足am+3=bn的项从小到大依次组成的数列,又记Sn为{cn}的前n项和,Tn为{an}的前n项和,求证:Sn≥Tn(n∈N+).
科目:高中数学 来源:湖南省十校联考2007届高三理科数学试题 题型:044
| |||||||||||||||
科目:高中数学 来源:2014届四川省高一下学期第二阶段数学试卷(解析版) 题型:解答题
已知数列 中,
中,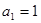 ,
,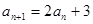 ,数列
,数列 中,
中,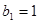 ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若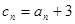 ,求数列
,求数列 的前
的前 项和
项和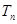 ;
;
【解析】第一问中利用数列的递推关系式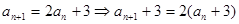
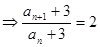 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中,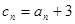 又
又 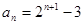

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)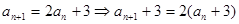
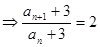 即数列
即数列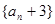 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列
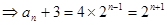
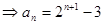 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3)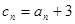 又
又 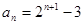


 ①
①  ②
②
①- ②得到

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com