已知点(a,b)在直线x+3y-2=0上,则u=3a+27b+3的最小值为 |
A、
B、3+2
C、6
D、9 |
相关习题
科目:高中数学
来源:
题型:
已知点(a,b)在直线x+3y-2=0上,则u=3a+27b+3的最小值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知点(a,b)在直线x+3y-2=0上,则u=3
a+27
b+3的最小值为( )
查看答案和解析>>
科目:高中数学
来源:2010-2011学年山东省德州市陵县一中高二期末数学模拟试卷3(解析版)
题型:选择题
已知点(a,b)在直线x+3y-2=0上,则u=3
a+27
b+3的最小值为( )
A.
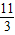
B.

C.6
D.9
查看答案和解析>>
科目:高中数学
来源:0115 期中题
题型:单选题
已知点(a,b)在直线x+3y-2=0上,则u=3a+27b+3的最小值为
A、

B、3+2

C、6
D、9
查看答案和解析>>
科目:高中数学
来源:
题型:

直线x+
y-2=0与圆x
2+y
2=4相交于C
1的圆心为(3,0),且经过点A(4,1).
(1)求圆C
1的方程;
(2)若圆C
2与圆C
1关于直线l对称,点B、D分别为圆C
1、C
2上任意一点,求|BD|的最小值;
(3)已知直线l上一点M在第一象限,两质点P、Q同时从原点出发,点P以每秒1个单位的速度沿x轴正方向运动,点Q以每秒
2个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C
1相切?
查看答案和解析>>
科目:高中数学
来源:
题型:
已知点A(-1,0)、B(1,0),△ABC的周长为2+2
.记动点C的轨迹为曲线W.
(1)直接写出W的方程(不写过程);
(2)经过点(0,
)且斜率为k的直线l与曲线W 有两个不同的交点P和Q,是否存在常数k,使得向量
+
与向量
(-,1)共线?如果存在,求出k的值;如果不存在,请说明理由.
(3)设W的左右焦点分别为F
1、F
2,点R在直线l:x-
y+8=0上.当∠F
1RF
2取最大值时,求
的值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖北省部分重点中学联考高二(上)期末数学试卷(解析版)
题型:解答题
已知点P(x
,y
)是渐近线为2x±3y=0且经过定点(6,2

)的双曲线C
1上的一动点,点Q是P关于双曲线C
1实轴A
1A
2的对称点,设直线PA
1与QA
2的交点为M(x,y),
(1)求双曲线C
1的方程;
(2)求动点M的轨迹C
2的方程;
(3)已知x轴上一定点N(1,0),过N点斜率不为0的直线L交C
2于A、B两点,x轴上是否存在定点 K(x
,0)使得∠AKN=∠BKN?若存在,求出点K的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知
f(x)=,曲线y=f(x)与直线l:4x+3y-5=0切于点A的横坐标为2,
g(x)=2x-.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间;
(3)若对于一切x∈[2,5],总存在x
1∈[m,n],使f(x)=g(x
1)成立,求n-m的最小值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知:△ABC中,顶点A(2,2),边AB上的中线CD所在直线的方程是x+y=0,边AC上的高BE所在直线的方程是x+3y+4=0.
(1)求点B、C的坐标;
(2)求△ABC的外接圆的方程.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知:△ABC中,顶点A(2,2),边AB上的中线CD所在直线的方程是x+y=0,边AC上的高BE所在直线的方程是x+3y+4=0.
(1)求点B、C的坐标; (2)求△ABC的外接圆的方程.
查看答案和解析>>

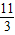



 直线x+
直线x+ )的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),
)的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),