
如下图所示,D是△ABC的边AB的中点, ,向量 ,向量 的夹角为120°,则 的夹角为120°,则 等于 等于 |
|
A.18+12  B.24 C.12 D.18-12  |
科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:013
如下图所示,D是△ABC的边AB上的中点,则向量![]() =( ).
=( ).

A.-![]() +
+![]()
![]()
B.-![]() -
-![]()
![]()
C.![]() -
-![]()
![]()
D.![]() +
+![]()
![]()
科目:高中数学 来源:山东省潍坊市2012届高考考前适应性训练(三模)数学文科试题 题型:013
如图1所示,正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面ACD⊥平面BCD(如图2),则下列结论中不正确的是
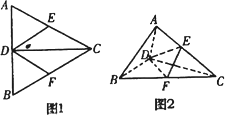
A.AB∥平面DEF
B.CD⊥平面ABD
C.EF⊥平面ACD
D.V三棱锥C-ABD=4V三棱锥C-DEF
科目:高中数学 来源:山东省潍坊市2012届高考考前适应性训练(三模)数学理科试题 题型:013
如图1所示,正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面ACD⊥平面BCD(如图2),则下列结论中不正确的是
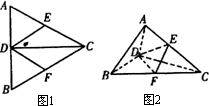
A.AB∥平面DEF
B.CD⊥平面ABD
C.EF⊥平面ACD
D.V三棱锥C-ABD=4V三棱锥C-DEF
科目:高中数学 来源: 题型:

科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷11 期末测试卷(A) 题型:022
如图所示,等腰直角三角形ABC的斜边AB在平面ABD内,D点是C点在平面ABD内的射影,现要从下列给出的条件中增加一个条件使得斜边上的中线CM平面ABD所成的角为45°:

(1)斜线AC与平面ABD所成的角为30°;
(2)线段CD的长与线段AM的长相等;
(3)![]()
(4)C点到平面ABD的距离等于M点到BC的距离;
则这一增加的条件的序号可以是________(写出全部可能条件的序号).
科目:高中数学 来源:2013-2014学年浙江省高三上学期第三次统练理科数学试卷(解析版) 题型:选择题
如图1所示,正△ABC中,CD是AB边上的高, E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )

A.AB//平面DEF B.CD⊥平面ABD
C.EF⊥平面ACD D.V三棱锥C—ABD=4V三棱锥C—DEF
科目:高中数学 来源: 题型:单选题
如图1所示,正△ABC中,CD是AB边上的高, E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )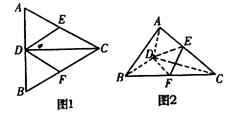
A.AB//平面DEF B.CD⊥平面ABD
C.EF⊥平面ACD D.V三棱锥C—ABD=4V三棱锥C—DEF
科目:高中数学 来源:不详 题型:单选题
 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com