已知数列{an}中,a1=1,an+1= (n∈N*),则a5等于 (n∈N*),则a5等于 |
A、
B、
C、
D、 |
相关习题
科目:高中数学
来源:
题型:解答题
已知数列{an}中,a1=1,an+1=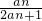 (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式an;
(2)设: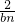 =
=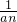 +1,求数列{bnbn+1}的前n项和Tn.
+1,求数列{bnbn+1}的前n项和Tn.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知数列{an}中,a1=1,an+1=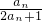 (n∈N).
(n∈N).
(1)求数列{an}的通项公式an;
(2)设: 求数列{bnbn+1}的前n项的和Tn;
求数列{bnbn+1}的前n项的和Tn;
(3)已知P=(1+b1)(1+b3)(1+b5)…(1+b2n-1),求证:Pn>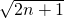 .
.
查看答案和解析>>
科目:高中数学
来源:广东省月考题
题型:解答题
已知数列{a
n}中,a
1=1,a
n+1=

(n∈N).
(1)求数列{a
n}的通项公式a
n;
(2)设:

求数列{b
nb
n+1}的前n项的和T
n;
(3)已知P=(1+b
1)(1+b
3)(1+b
5)…(1+b
2n﹣1),求证:P
n>

.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省梅州市梅州中学高三(上)第二次月考数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n}中,a
1=1,a
n+1=

(n∈N).
(1)求数列{a
n}的通项公式a
n;
(2)设:

求数列{b
nb
n+1}的前n项的和T
n;
(3)已知P=(1+b
1)(1+b
3)(1+b
5)…(1+b2
n-1),求证:Pn>

.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省珠海市高三(上)期末数学试卷(解析版)
题型:解答题
已知数列{a
n}中,a
1=1,a
n+1=

(n∈N).
(1)求数列{a
n}的通项公式a
n;
(2)设:

求数列{b
nb
n+1}的前n项的和T
n;
(3)已知P=(1+b
1)(1+b
3)(1+b
5)…(1+b2
n-1),求证:Pn>
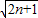
.
查看答案和解析>>
科目:高中数学
来源:专项题
题型:单选题
已知数列{a
n}中,a
1=1,a
n+1=
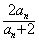
(n∈N*),则a
5等于
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{an}中,a1=1,an+1(2+an)=2an(n∈N*),
(Ⅰ)求a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ)记Tn=a1a2+a2a3+…+an-1an(n≥2),试判断Tn与2的大小,并说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知数列{an}中,a1=1,an+1(2+an)=2an(n∈N*),
(Ⅰ)求a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ)记Tn=a1a2+a2a3+…+an-1an(n≥2),试判断Tn与2的大小,并说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列{an}中,a1=1,an+1(2+an)=2an(n∈N*),
(Ⅰ)求a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ)记Tn=a1a2+a2a3+…+an-1an(n≥2),试判断Tn与2的大小,并说明理由.
查看答案和解析>>
科目:高中数学
来源:2013-2014学年广西桂林十八中高三(上)第一次月考数学试卷(理科)(解析版)
题型:选择题
已知数列{a
n}中,a
1=2,a
n+1=

(n∈N
*),则a
4=( )
A.

B.

C.

D.

查看答案和解析>>

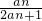 (n∈N*).
(n∈N*).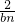 =
=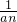 +1,求数列{bnbn+1}的前n项和Tn.
+1,求数列{bnbn+1}的前n项和Tn.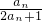 (n∈N).
(n∈N). 求数列{bnbn+1}的前n项的和Tn;
求数列{bnbn+1}的前n项的和Tn;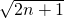 .
. (n∈N).
(n∈N). 求数列{bnbn+1}的前n项的和Tn;
求数列{bnbn+1}的前n项的和Tn; .
. (n∈N).
(n∈N). 求数列{bnbn+1}的前n项的和Tn;
求数列{bnbn+1}的前n项的和Tn; .
. (n∈N).
(n∈N). 求数列{bnbn+1}的前n项的和Tn;
求数列{bnbn+1}的前n项的和Tn;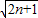 .
. (n∈N*),则a4=( )
(n∈N*),则a4=( )


