练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知关于x的三次函数f（x）=在区间（1，2）上有且只有一个极大值，则b-a的取值范围是

    A.（-1，+∞）
    B.（-2，+∞）
    C.（-3，+∞）
    D.（-4，+∞）
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：辽宁省模拟题 题型：单选题

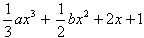    已知关于x的三次函数f（x）=在区间（1，2）上有且只有一个极大值，则b-a的取值范围是
    [     ]
    A.（-1，+∞）
    B.（-2，+∞）
    C.（-3，+∞）
    D.（-4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知关于x的三次函数f(x)=
    1
    3
    ax3+
    1
    2
    bx2+2x+1    在区间（1，2）上只有极大值，则b-a的取值范围是（　　）
    A、（-1，+∞）
    B、（-2，+∞）
    C、（-3，+∞）
    D、（-4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于一般的三次函数f（x）=ax3+bx2+cx+d，（a≠0）定义：设f''（x）是函数y=f（x）的导函数y=f'（x）的导数．若f''（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”，现已知：g（x）=（x-a）（x-b）（x-c），请解答下列问题：
    （Ⅰ）．若y=g（x）是R上的增函数，求证a=b=c；
    （Ⅱ）在（Ⅰ）．的条件下，求函数y=g（x）的“拐点”A的坐标，并证明函数y=g（x）的图象关于“拐点”A成中心对称．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    对于一般的三次函数f（x）=ax3+bx2+cx+d，（a≠0）定义：设f''（x）是函数y=f（x）的导函数y=f'（x）的导数．若f''（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”，现已知：g（x）=（x-a）（x-b）（x-c），请解答下列问题：
    （Ⅰ）．若y=g（x）是R上的增函数，求证a=b=c；
    （Ⅱ）在（Ⅰ）．的条件下，求函数y=g（x）的“拐点”A的坐标，并证明函数y=g（x）的图象关于“拐点”A成中心对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f为实系数三次多项式函数．已知五个方程式的相异实根个数如下表所述﹕
    f（x）-20=01f（x）+10=01
    f（x）-10=03f（x）+20=01
    f（x）=03
    关于f的极小值α﹐试问下列选项是正确的﹖（　　）
    A、0＜α＜10
    B、-20＜α＜-10
    C、-10＜α＜0
    D、α不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中：
    ①集合A={ x|0≤x＜3且x∈N }的真子集的个数是8；
    ②关于x的一元二次方程x2+mx+2m+1=0一个根大于1，一个根小于1，则实数m的取值范围m＜-
    2
    3
    ；
    ③函数f（x）=x2+（3a+1）x+2a在 （-∞，4）上为减函数，则实数a的取值范围是a≤3；
    ④已知函数y=4x-4•2x+1（-1≤x≤2），则函数的值域为[-
    3
    4
    ，1]；
    ⑤定义在（-1，0）的函数f（x）=log（2a）（x+1）满足f（x）＞0的a的取值范围是（0，
    1
    2
    ）；
    ⑥将三个数：x=20.2，y=(
    1
    2
    )2    ，z=log2
    1
    2
    ，
    按从大到小排列正确的是z＞x＞y，其中正确的有
    ②⑤
    ②⑤
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省宣城市六校高三第三次联考数学试卷（理科）（解析版） 题型：解答题

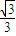    已知三次函数f（x）=ax3+bx2+cx+d（a≠0）为R上奇函数，且在x=处取得极值-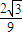．记函数图象为曲线C．
    （Ⅰ）求函数f（x）的表达式；
    （Ⅱ）设曲线C与其在点P1（1，f（1））处的切线交于另一点P2（x2，f（x2）），线段P1P2与曲线C所围成封闭图形的面积记为S1，求S1的值；
    （Ⅲ） 在（Ⅱ）的条件下，设曲线C与其在点P2处的切线交于另一点P3（x3，f（x3）），线段P2P3与曲线C所围成封闭图形的面积记为S2，…，按此方法依次做下去，即设曲线C与其在点Pn（xn，f（xn））处的切线交于另一点Pn+1（xn+1，f（xn+1）），线段PnPn+1与曲线C所围成封闭图形的面积记为Sn，试求Sn关于n的表达式．

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（大纲卷解析版） 题型：解答题

    已知函数

    （I）     讨论f（x）的单调性；

    （II）   设f（x）有两个极值点若过两点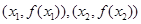的直线I与x轴的交点在曲线上，求α的值。

    【解析】本试题考查了导数在研究函数中的运用。第一就是三次函数，通过求解导数，求解单调区间。另外就是运用极值的概念，求解参数值的运用。

    【点评】试题分为两问，题面比较简单，给出的函数比较常规，，这一点对于同学们来说没有难度但是解决的关键还是要看导数的符号的实质不变，求解单调区间。第二问中，运用极值的问题，和直线方程的知识求解交点，得到参数的值。

    （1）

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中：
    ①集合A={ x|0≤x＜3且x∈N }的真子集的个数是8；
    ②将三个数：x=20.2，y=(
    1
    2
    )2    ，z=log2
    1
    2
    按从大到小排列正确的是z＞x＞y；
    ③函数f（x）=x2+（3a+1）x+2a在 （-∞，4）上为减函数，则实数a的取值范围是a≤-3；
    ④已知函数y=4x-4•2x+1（-1≤x≤2），则函数的值域为[-
    3
    4
    ，1]；
    ⑤定义在（-1，0）的函数f（x）=log（2a）（x+1）满足f（x）＞0的实数a的取值范围是0＜a＜
    1
    2
    ；
    ⑥关于x的一元二次方程x2+mx+2m+1=0一个根大于1，一个根小于1，则实数m的取值范围m＜-
    2
    3
    ；
    其中正确的有
    ③⑤⑥
    ③⑤⑥
    （请把所有满足题意的序号都填在横线上）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    下列命题中：
    ①集合A={ x|0≤x＜3且x∈N }的真子集的个数是8；
    ②将三个数：x=20.2，y=(
    1
    2
    )2    ，z=log2
    1
    2
    按从大到小排列正确的是z＞x＞y；
    ③函数f（x）=x2+（3a+1）x+2a在 （-∞，4）上为减函数，则实数a的取值范围是a≤-3；
    ④已知函数y=4x-4•2x+1（-1≤x≤2），则函数的值域为[-
    3
    4
    ，1]；
    ⑤定义在（-1，0）的函数f（x）=log（2a）（x+1）满足f（x）＞0的实数a的取值范围是0＜a＜
    1
    2
    ；
    ⑥关于x的一元二次方程x2+mx+2m+1=0一个根大于1，一个根小于1，则实数m的取值范围m＜-
    2
    3
    ；
    其中正确的有______（请把所有满足题意的序号都填在横线上）

    查看答案和解析>>


    同步练习册答案