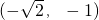| 已知函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为 |
A.(0,1)
B.
C.
D. |
相关习题
科目:高中数学
来源:专项题
题型:单选题
已知函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为
查看答案和解析>>
科目:高中数学
来源:四川省南山中学2011-2012学年高二五月月考数学文科试题
题型:013
已知函数f(x)的导函数为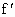 (x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为
(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为
[ ]
B.(1, )
)
C.(-2,- )
)
查看答案和解析>>
科目:高中数学
来源:
题型:
已知奇函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为( )
| A、(0,1) |
| B、(1, ) |
| C、(-2, -) |
| D、(1, )∪(-, -1) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知奇函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x
2)<0,则实数x的取值范围为( )
| A.(0,1) | B.(1, ) |
| C.(-2, -) | D.(1, )∪(-, -1) |
查看答案和解析>>
科目:高中数学
来源:合肥模拟
题型:单选题
已知向量
=(sinx,cosx),=(cosx,cosx),
f(x)=•-,下面关于函数f(x)的导函数f'(x)说法中错误的是( )
| A.函数最小正周期是π |
| B.函数在区间(0,)为减函数 |
| C.函数的图象关于直线x=对称 |
| D.图象可由函数y=2sin2x向左平移个单位长度得到 |
查看答案和解析>>
科目:高中数学
来源:2009-2010学年江西省宜春市宜丰中学高二第八次模拟数学试卷(理科)(解析版)
题型:选择题
已知奇函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x
2)<0,则实数x的取值范围为( )
A.(0,1)
B.
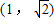
C.
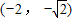
D.

∪

查看答案和解析>>
科目:高中数学
来源:2010-2011学年广东省中山市高三(上)期末数学试卷(理科)(解析版)
题型:选择题
已知奇函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x
2)<0,则实数x的取值范围为( )
A.(0,1)
B.

C.

D.

∪
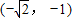
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知奇函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为
- A.
(0,1)
- B.
- C.
- D.
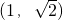
∪
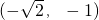
查看答案和解析>>
科目:高中数学
来源:
题型:
(2010•合肥模拟)已知向量
=(sinx,cosx),=(cosx,cosx),
f(x)=•-,下面关于函数f(x)的导函数f'(x)说法中错误的是( )
|
|
|
|
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
已知函数y=f(x)的导函数为f′(x)=5+cosx,且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围是________.
查看答案和解析>>




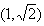
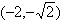

![]() (x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为
(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为![]() )
)![]() )
)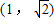
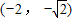
 ∪
∪


 ∪
∪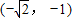
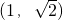
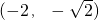
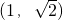 ∪
∪