
科目:初中数学 来源: 题型:
| AD |
| AB |
| 1 |
| 3 |
| 3 |
| 4 |
| CE |
| EA |
A、
| ||
B、
| ||
C、
| ||
D、
|
科目:初中数学 来源:不详 题型:单选题
| AD |
| AB |
| 1 |
| 3 |
| 3 |
| 4 |
| CE |
| EA |
A.
| B.
| C.
| D.
|
科目:初中数学 来源:初中数学竞赛专项训练09:面积及等积变换(解析版) 题型:选择题
 =
= ,若在边AC上取一点E,使四边形DECB的面积为
,若在边AC上取一点E,使四边形DECB的面积为 ,则
,则 的值为( )
的值为( )



科目:初中数学 来源: 题型:解答题
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为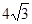 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.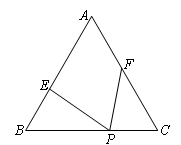
科目:初中数学 来源:不详 题型:解答题
 时,求x的值.
时,求x的值.
科目:初中数学 来源: 题型:解答题
 已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y. 时,求x的值.②四边形AEPF的面积是否存在最大值?若存在,请直接写出面积的最大值;若不存在,请说明理由.
时,求x的值.②四边形AEPF的面积是否存在最大值?若存在,请直接写出面积的最大值;若不存在,请说明理由.科目:初中数学 来源:2012年10月中考数学模拟试卷(9)(解析版) 题型:选择题

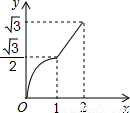
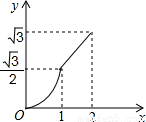
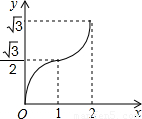
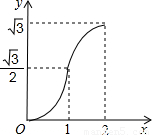
科目:初中数学 来源:2012年重庆市渝北区中考数学一模试卷(解析版) 题型:选择题





科目:初中数学 来源:2012年重庆市开县西街中学中考数学一模试卷(解析版) 题型:选择题
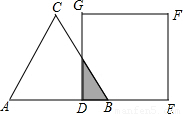
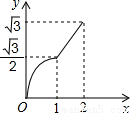
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com