
科目:初中数学 来源: 题型:
如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在![]() 上找一点P,使得
上找一点P,使得![]() =
=![]() ,以下是甲、乙两人的作法:
,以下是甲、乙两人的作法:
甲:(1)取AB中点D
(2)过D作直线AC的并行线,交![]() 于P,则P即为所求
于P,则P即为所求
乙:(1)取AC中点E
(2)过E作直线AB的并行线,交![]() 于P,则P即为所求
于P,则P即为所求
对于甲、乙两人的作法,下列判断何者正确?( )

|
| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误C | D. | 甲错误,乙正确 |
科目:初中数学 来源:2012年台湾省中考数学试卷(解析版) 题型:选择题
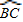 上找一点P,使得
上找一点P,使得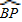 =
= ,以下是甲、乙两人的作法:
,以下是甲、乙两人的作法: 于P,则P即为所求
于P,则P即为所求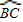 于P,则P即为所求
于P,则P即为所求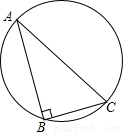
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.4个 | B.3个 | C.2个 | D.1个 |
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:2011年浙江省宁波市初中数学复习评估练习(五)(解析版) 题型:选择题
科目:初中数学 来源: 题型:
科目:初中数学 来源:2013年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
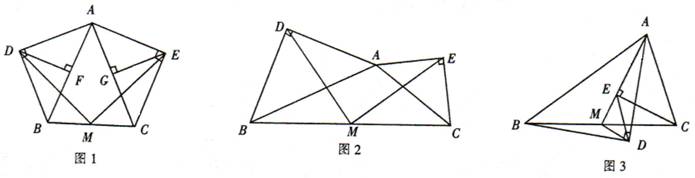
●操作发现:
在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是 (填序号即可)
①AF=AG= AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
●数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;
●类比探索:
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,试判断△MED的形状.
答: .
科目:初中数学 来源:不详 题型:单选题
| A.①和② | B.②和③ | C.①和③ | D.①②③ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com