
科目:初中数学 来源: 题型:
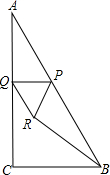 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC与Q,以PQ为边向下作等边三角形PQR,设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC与Q,以PQ为边向下作等边三角形PQR,设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.科目:初中数学 来源: 题型:解答题
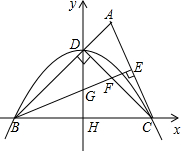 如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系.
如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系. CE吗?若存在,请证明;若不存在,请说明理由;
CE吗?若存在,请证明;若不存在,请说明理由;科目:初中数学 来源:2011年重庆市南岸区中考数学一模试卷(解析版) 题型:解答题
 CE吗?若存在,请证明;若不存在,请说明理由;
CE吗?若存在,请证明;若不存在,请说明理由;
科目:初中数学 来源: 题型:解答题
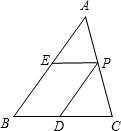 BC交AB于点E.
BC交AB于点E.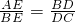 ;
;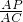 的值.
的值.科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC于Q,以PQ为边向下作等边三角形PQR.设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC于Q,以PQ为边向下作等边三角形PQR.设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.科目:初中数学 来源:2012年河南省中招考试说明解密预测数学试卷(六)(解析版) 题型:解答题

科目:初中数学 来源:2012年安徽省中考数学模拟试卷(十二)(解析版) 题型:解答题

科目:初中数学 来源:2012年河南省平顶山市中考数学一模试卷(解析版) 题型:解答题

科目:初中数学 来源:2012年重庆市中考解密预测数学试卷(解析版) 题型:解答题

科目:初中数学 来源:2011年山东省德州市陵县中考数学一模试卷(解析版) 题型:解答题
 ;
; 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com