练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若直线l的斜率为-2，并且直线l过点（3，-1），则直线l的方程是（　　）
    A．2x+y-5=0B．2x+y+7=0C．2x+y-7=0D．-2x+y-5=0
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    3、若直线l的斜率为-2，并且直线l过点（3，-1），则直线l的方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若直线l的斜率为-2，并且直线l过点（3，-1），则直线l的方程是（　　）
    A．2x+y-5=0B．2x+y+7=0C．2x+y-7=0D．-2x+y-5=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    直线l过点P（-2，1）且斜率为k（k＞1），将直线l绕P点按逆时针方向旋转45°得直线m，若直线l和m分别与y轴交于Q，R两点．
    （1）用k表示直线m的斜率；
    （2）当k为何值时，△PQR的面积最小？并求出面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    直线l过点P（-2，1）且斜率为k（k＞1），将直线l绕P点按逆时针方向旋转45°得直线m，若直线l和m分别与y轴交于Q，R两点．
    （1）用k表示直线m的斜率；
    （2）当k为何值时，△PQR的面积最小？并求出面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：江苏月考题 题型：解答题

    直线l过点P（﹣2，1）且斜率为k（k＞1），将直线l绕P点按逆时针方向旋转45°得直线m，若直线l和m分别与y轴交于Q，R两点．
    （1）用k表示直线m的斜率；
    （2）当k为何值时，△PQR的面积最小？并求出面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省重点中学高二（上）10月月考数学试卷（解析版） 题型：解答题

    直线l过点P（-2，1）且斜率为k（k＞1），将直线l绕P点按逆时针方向旋转45°得直线m，若直线l和m分别与y轴交于Q，R两点．
    （1）用k表示直线m的斜率；
    （2）当k为何值时，△PQR的面积最小？并求出面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：高二数学 教学与测试 题型：044

    直线l过P(－2，1)且斜率为k(k＞1)．将直线l绕P点按逆时针方向旋转得直线m，若直线l和直线m分别与y轴交于Q，R点，则当k为何值时，△PQR的面积最小？并求出面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源：江苏省重点中学2011-2012学年高二10月月考数学试题 题型：044

    直线l过点P(－2，1)且斜率为k(k＞1)，将直线l绕P点按逆时针方向旋转45°得直线m，若直线l和m分别与y轴交于Q，R两点．

    (1)用k表示直线m的斜率；

    (2)当k为何值时，△PQR的面积最小？并求出面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

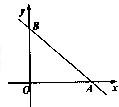    精英家教网如图直线l与x轴、y轴的正半轴分别交于A、B两点，OA、OB的长分别是关于x的方程x2-14x+4（AB+2）=0的两个根（OA＜OB），P为直线l上异于A、B两点之间的一动点． 且PQ∥OB交OA于点Q．
    （1）求直线lAB斜率的大小；
    （2）若S△PAQ=
    13
    S四OQPB    时，请你确定P点在AB上的位置，并求出线段PQ的长；
    （3）在y轴上是否存在点M，使△MPQ为等腰直角三角形，若存在，求出点M的坐标；
    若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A、B两点．
    （1）若|AF|=4，求点A的坐标；
    （2）设直线l的斜率为k，当线段AB的长等于5时，求k的值．
    （3）求抛物线y2=4x上一点P到直线2x-y+4=0的距离的最小值．并求此时点P的坐标．

    查看答案和解析>>


    同步练习册答案