
已知数列{an},若点(n,an)(n∈N*)在一次函数y=k(x-8)+4的图象上,则数列{an}的前15项和S15=( )
|
科目:高中数学 来源:不详 题型:单选题
| A.12 | B.32 | C.60 | D.120 |
科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:解答题
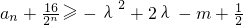 对一切正整数n和实数λ均恒成立,求整数m的最小值.
对一切正整数n和实数λ均恒成立,求整数m的最小值.科目:高中数学 来源: 题型:解答题
科目:高中数学 来源:0123 月考题 题型:解答题
 ,求证:对任意的m,n∈N*,向量
,求证:对任意的m,n∈N*,向量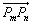 与向量
与向量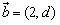 共线;
共线;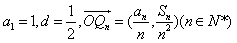 ,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。
,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。 科目:高中数学 来源:不详 题型:解答题
科目:高中数学 来源:2012-2013学年湖北省武汉二中高一(下)期中数学试卷(文科)(解析版) 题型:解答题
 )在直线y=
)在直线y= x+
x+ 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153. ,数列{cn}的前n项和为Tn,求Tn及使不等式Tn<
,数列{cn}的前n项和为Tn,求Tn及使不等式Tn< 对一切n都成立的最小正整数k的值;
对一切n都成立的最小正整数k的值; 问是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值; 若不存在,请说明理由.
问是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值; 若不存在,请说明理由.科目:高中数学 来源:2009年湖北省武汉市武昌区高三元月调考数学试卷(文科)(解析版) 题型:解答题
 ,求证:对任意的m,n∈N*,向量
,求证:对任意的m,n∈N*,向量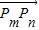 与向量
与向量 共线;
共线; ,
,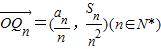 ,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上.
,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上.科目:高中数学 来源:2010-2011学年四川省成都外国语学校高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
 ,求证:对任意的m,n∈N*,向量
,求证:对任意的m,n∈N*,向量 与向量
与向量 共线;
共线; ,
, ,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上.
,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com