
某工厂某种产品的产量x(千件)与单位成本y(万元)之间的关系满足y=60-2.5x,则以下说法正确的是( )
|
科目:高中数学 来源:不详 题型:单选题
| A.产品每增加1000件,单位成本下降2.5万元 |
| B.产品每减少1100件,单位成本上升2.5万元 |
| C.产品每增加1000件,单位成本上升2.5万元 |
| D.产品每减少1000件,单位成本下降2.5万元 |
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:陕西省期中题 题型:单选题
科目:高中数学 来源:2013-2014学年上海市长宁区高三上学期教学质量检测理科数学试卷(解析版) 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
科目:高中数学 来源:2013-2014学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求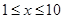 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是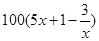 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求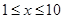 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是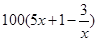 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
科目:高中数学 来源:不详 题型:解答题
 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元.科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 10000 |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com