
下列命题为真命题的是( )
|
科目:高中数学 来源:2012-2013学年河北省石家庄市正定县弘文中学高三(上)期中数学试卷(文科)(解析版) 题型:选择题

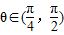 ,则f(sinθ)>f(cosθ)
,则f(sinθ)>f(cosθ) 的图象是关于点
的图象是关于点 成中心对称图形
成中心对称图形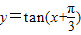 的图象时关于直线
的图象时关于直线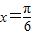 成轴对称图形
成轴对称图形科目:高中数学 来源:不详 题型:单选题
A.若锐角α,β满足cosα>sinβ,则α+β>
| ||||
B.若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈(
| ||||
C.函数y=cos(x+
| ||||
D.函数y=tan(x+
|
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试3 题型:选择题
设命题P:在直角坐标平面内,点M(sinα,cosα)与N(1,2)在直线x+y-2=0的
两侧;命题q:若向是a,b满足a·b>0,则a与b的夹角为锐角.下列结论正确的是( )
A.“p∨q” 为真 “p∧q”为真
B.“p∨q” 为真 “p∧q”为假
C.“p∨q” 为假 “p∧q”为真
D.“p∨q” 为假 “p∧q”为假
科目:高中数学 来源:2012-2013学年安徽省蚌埠二中高三(上)暑期测试数学试卷(文科)(解析版) 题型:填空题
 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为 ;
; ;
; 的图象,只需将
的图象,只需将 的图象向右平移
的图象向右平移 个单位.
个单位. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.科目:高中数学 来源:2012-2013学年安徽省蚌埠二中高三(上)暑期测试数学试卷(文科)(解析版) 题型:填空题
 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为 ;
; ;
;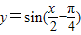 的图象,只需将
的图象,只需将 的图象向右平移
的图象向右平移 个单位.
个单位.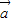 和
和 满足|
满足| |=|
|=| |=|
|=|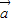 -
- |,则
|,则 与
与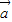 +
+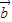 的夹角为60°.
的夹角为60°.科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| OP |
| OA |
| OB |
| OC |
| AB |
| AC |
| AB |
| AC |
科目:高中数学 来源:2013年安徽省合肥市高考数学二模试卷(文科)(解析版) 题型:填空题
 与向量
与向量 共线,则存在实数λ使
共线,则存在实数λ使 =λ
=λ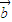 (λ∈R);
(λ∈R); ,
, 为单位向量,其夹角为θ,若|
为单位向量,其夹角为θ,若| -
- |>1,则
|>1,则 <θ≤π;
<θ≤π; •
• =0,
=0,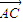 •
•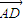 =0,
=0, •
• =0则△BCD 一定是锐角三角形;
=0则△BCD 一定是锐角三角形;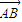 ,
,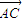 ,
, 满足
满足 =
= +
+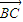 ,则
,则 与
与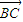 同向;
同向;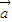 ∥
∥ ,
, ∥
∥ ,则
,则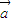 ∥
∥ .
.科目:高中数学 来源:合肥二模 题型:填空题
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| AB |
| AC |
| AC |
| AD |
| AB |
| AD |
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
| AC |
| BC |
| a |
| b |
| b |
| c |
| a |
| c |
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| AB |
| AC |
| AC |
| AD |
| AB |
| AD |
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
| AC |
| BC |
| a |
| b |
| b |
| c |
| a |
| c |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com