
在平面直角坐标系中,若把抛物线y=x2-4x-21先向右平移2个单位长度,再向上平移5个单位长度,则经过这两次平移后所得到的抛物线的顶点坐标是( )
|
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.(0,-20) | B.(0,-30) | C.(4,-20) | D.(4,-30) |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:解答题
 x+
x+ 交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.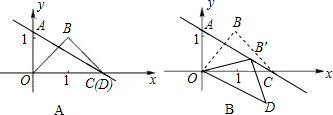
科目:初中数学 来源: 题型:解答题
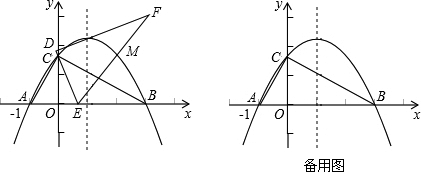
科目:初中数学 来源: 题型:
如图在平面直角坐标系中,点A的坐标为(1,![]() ) ,△AOB的面积是
) ,△AOB的面积是![]() .
.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中![]() 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作![]() 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
 |
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,抛物线![]() 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.

【解析】(1)把点M、N的坐标点入抛物线,即可求得,a,b
(2)由△DMN为直角三角形,求出点D的坐标,然后求出直线MD的解析式,即可求得点P的坐标
(3)逆向思维,设存在点Q进行解答
科目:初中数学 来源: 题型:
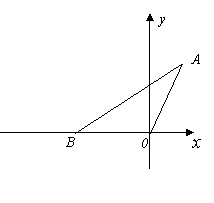
在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B,C的坐标:B( , ),C( , );
(2)求经过A,B,C三点的抛物线解析式;
(3)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A,B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(2)中的抛物线交于第一象限的点M.当AE=2时,抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
 |
科目:初中数学 来源:2012年初中毕业升学考试(福建龙岩卷)数学(带解析) 题型:解答题
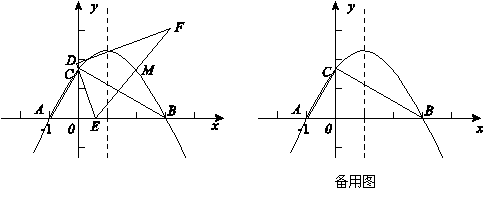
在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
科目:初中数学 来源:2013-2014学年福建龙岩永定仙师中学九年级上第17周周末测试数学卷(解析版) 题型:解答题
在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).

(1)请直接写出点B,C的坐标:B( , ),C( , );
(2)求经过A,B,C三点的抛物线解析式;
(3)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A,B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(2)中的抛物线交于第一象限的点M.当AE=2时,抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com