
科目:高中数学 来源: 题型:
| π | 3 |
科目:高中数学 来源: 题型:
| x |
| 2 |
| π |
| 6 |
科目:高中数学 来源:不详 题型:解答题
| x |
| 2 |
| π |
| 6 |

科目:高中数学 来源:山东省日照一中2011-2012学年高一下学期模块笔试(学段调研)数学试题 题型:044
已知O为坐标原点,![]() =(2cos2x,1),
=(2cos2x,1),![]() =(1,
=(1,![]() sin2x+a)(x∈R,a∈R,a是常数),若y=
sin2x+a)(x∈R,a∈R,a是常数),若y=![]() ·
·![]() .
.
(1)求y关于x的函数关系式f(x);
(2)若f(x)的最大值为2,求a的值;
(3)利用(2)的结论,用“五点法”作出函数f(x)在长度为一个周期的闭区间上的简图,并指出函数f(x)的单调区间.
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
科目:高中数学 来源:2012-2013学年内蒙古包头33中高一(下)期末数学试卷(文科)(解析版) 题型:解答题

科目:高中数学 来源:山东省期中题 题型:解答题
 为坐标原点,
为坐标原点,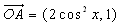 ,
,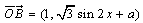 (
( ,a是常数),若
,a是常数),若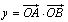 。
。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com