
对任意的函数y=f(x)在同-直角坐标系中,函数y=f(x+1)与函数y=f(-x-1)的图象恒( )
|
科目:高中数学 来源:不详 题型:单选题
| A.关于x轴对称 | B.关于直线x=1对称 |
| C.关于直线x=-1对称 | D.关于Y轴对称 |
科目:高中数学 来源:2013年高考数学压轴小题训练:函数的图象(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:2010-2011学年浙江省绍兴市稽山中学高一(下)期中数学试卷(解析版) 题型:解答题

 ,且
,且 ,
, ,其中ω>0对任意的t∈R,函数f(x)在x∈[t,t+π)的图象与直线y=-1有且仅有两个不同的交点,试确定ω的值(不必证明),并求出函数f(x)的单调增区间.
,其中ω>0对任意的t∈R,函数f(x)在x∈[t,t+π)的图象与直线y=-1有且仅有两个不同的交点,试确定ω的值(不必证明),并求出函数f(x)的单调增区间.科目:高中数学 来源: 题型:解答题
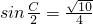
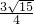 ,且
,且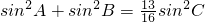 ,
,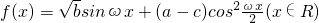 ,其中ω>0对任意的t∈R,函数f(x)在x∈[t,t+π)的图象与直线y=-1有且仅有两个不同的交点,试确定ω的值(不必证明),并求出函数f(x)的单调增区间.
,其中ω>0对任意的t∈R,函数f(x)在x∈[t,t+π)的图象与直线y=-1有且仅有两个不同的交点,试确定ω的值(不必证明),并求出函数f(x)的单调增区间.科目:高中数学 来源: 题型:
| C |
| 2 |
| ||
| 4 |
3
| ||
| 4 |
| 13 |
| 16 |
| b |
| ωx |
| 2 |
科目:高中数学 来源:四川省月考题 题型:填空题
 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“ >0”;
>0”;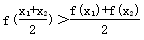 ;
;科目:高中数学 来源:2009-2010学年四川省眉山市仁寿一中高三(下)3月月考数学试卷(文理合卷)(解析版) 题型:填空题
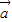 ,
, 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“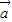 •
•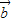 >0”;
>0”;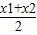 )>
)>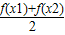 ;
;科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com