
已知△ABC三边之比为3:4:5,与其相似的△DEF的周长为24,则S△DEF为( )
|
科目:初中数学 来源:2008-2009学年湖南省益阳市桃江县浮邱山乡中心校联考九年级(上)期末数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:阅读理解
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边÷腰=![]() 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
|

|
|
 <A
<A <
<
|
|
|
|
(3)如图2,已知sinA=![]() ,其中∠A为锐角,
,其中∠A为锐角,
试求sadA的值。(兰州中考题改编) 图1 图2
科目:初中数学 来源: 题型:阅读理解
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边÷腰=![]() 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:

|

|
(2)对于![]() <A<
<A<![]() ,∠A的正对值sadA的
,∠A的正对值sadA的
|
|
|
|
(3)如右图,已知sinA=![]() ,其中∠A为锐角,
,其中∠A为锐角,
试求sadA的值。
科目:初中数学 来源: 题型:阅读理解
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边÷腰=![]() 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:

|

|
(2)对于![]() <A<
<A<![]() ,∠A的正对值sadA的
,∠A的正对值sadA的
|
|
|
|
(3)如右图,已知sinA=![]() ,其中∠A为锐角,
,其中∠A为锐角,
试求sadA的值。
科目:初中数学 来源: 题型:
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
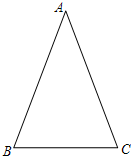
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad ![]() 的值为( )A.
的值为( )A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
(2)对于![]() ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知![]() ,其中
,其中![]() 为锐角,试求sad
为锐角,试求sad![]() 的值.
的值.

科目:初中数学 来源: 题型:
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与![]() 腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=![]() .容易知道一个角的大小与这个角的正对值也是
.容易知道一个角的大小与这个角的正对值也是![]() 相互唯一确定的.
相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad ![]() 的值为( )A.
的值为( )A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
(2)对于![]() ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知![]() ,其中
,其中![]() 为锐角,试求sad
为锐角,试求sad![]() 的值.
的值.

科目:初中数学 来源: 题型:
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.| 底边 |
| 腰 |
| BC |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com