练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    满足a，b∈{-1，0，1，2}，且关于x的方程ax2+2x+b=0有实数解的有序数对的个数为（　　）
    A．14B．13C．12D．10
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：福建 题型：单选题

    满足a，b∈{-1，0，1，2}，且关于x的方程ax2+2x+b=0有实数解的有序数对的个数为（　　）
    A．14B．13C．12D．10

    查看答案和解析>>

    科目：高中数学 来源：2013年福建省高考数学试卷（理科）（解析版） 题型：选择题

    满足a，b∈{-1，0，1，2}，且关于x的方程ax2+2x+b=0有实数解的有序数对的个数为（ ）
    A．14
    B．13
    C．12
    D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•福建）满足a，b∈{-1，0，1，2}，且关于x的方程ax2+2x+b=0有实数解的有序数对的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    满足a，b∈{－1，0，1，2}，且关于x的方程有实数解的有序数对(a，b)的个数为(　　)
    A．14
    B．13
    C．12
    D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    满足a，b∈{－1，0，1，2}，且关于x的方程有实数解的有序数对(a，b)的个数为(　　)

    A．14
    B．13
    C．12
    D．10

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习真题感悟1-7练习卷（解析版） 题型：选择题

    满足a，b∈{－1,0,1,2}，且关于x的方程ax2＋2x＋b＝0有实数解的有序数对(a，b)的个数为(　　)．

    A．14 B．13

    C．12 D．10

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    满足a，b∈{－1,0,1,2}，且关于x的方程ax2＋2x＋b＝0有实数解的有序数对(a，b)的个数为(　　)．

    A．14 B．13
    C．12 D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

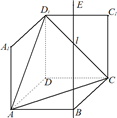    精英家教网如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
    （Ⅰ） 设二面角E-AC-D1的大小为θ，若
    π
    4
    ≤θ≤
    π
    3
    ，求线段BE长的取值范围；
    （Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
    D1P
    PE
    与BE之间满足的关系式，并证明：当0＜BE＜a时，恒有
    D1P
    PE
    ＜1．

    查看答案和解析>>

    科目：高中数学 来源：浙江省十校联合体2011－2012学年高二上学期期末联考数学理科试题 题型：044

    已知点A(0，1)，B(0，－1)，P是一个动点，且直线PA，PB的斜率之积为．

    (1)求动点P的轨迹方程C；

    (2)C上一动点P(x0，y0)关于直线y＝2x的对称点为P1(x1，y1)，求3x1－4y1的取值范围；

    (3)设Q(2，0)，过点(－1，0)的直线l交C于M，N两点，△QMN的面积记为S，若对满足条件的任意直线l，不等式S≤λtan∠MQN恒成立，求λ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求分别满足下列条件的直线l的方程：

    (1)斜率是，且与两坐标轴围成的三角形的面积是6；

    (2)经过两点A(1,0)，B(m,1)；

    (3)经过点(4，－3)，且在两坐标轴上的截距的绝对值相等．

    [分析]欲求直线的方程，关键是根据已知条件选择一种最合适的形式．

    查看答案和解析>>


    同步练习册答案