练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    定义：f（a，b）=（b，a），g（m，n）=（-m，-n）．例如f（2，3）=（3，2），g（-1，-4）=（1，4）．则g[f（-5，6）]等于（　　）
    A．（-6，5）B．（-5，-6）C．（6，-5）D．（-5，6）
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

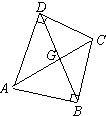    21、定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．（1）如图，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段
    AC
    ．
    （2）①在损矩形ABCD内是否存在点O，使得A、B、C、D四个点都在以O为圆心的同一圆上，如果有，请指出点O的具体位置；
    ②如图，直接写出符合损矩形ABCD的两个结论（不能再添加任何线段或点）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：已知反比例函数y=
    k1
    x
    与y=
    k2
    x
    ，如果存在函数y=
    		k1k2
    x
    （k1k2＞0）则称函数y=
    		k1k2
    x
    为这两个函数的中和函数．
    （1）试写出一对函数，使得它的中和函数为y=
    2
    x
    ，并且其中一个函数满足：当x＜0时，y随x的增大而增大．
    （2）函数y=
    -3
    x
    和y=
    -12
    x
    的中和函数y=
    k
    x
    的图象和函数y=2x的图象相交于两点，试求当y=
    k
    x
    的函数值大于y=2x的函数值时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：如果一个图形经过分割，能分为4个与自身相似的图形，我们称它为“能四阶自相似分割图形”．如图1，任意△ABC取各边的中点D、E、F，连接DE、EF、DF，分得的△ADF、△BDE、△DEF、△CEF显然都与△ABC相似，则任意△ABC是“能四阶自相似分割图形”．
    精英家教网
    （1）小明发现：任意矩形ABCD（如图2）也是“能四阶自相似分割图形”．请你利用尺规作图作出分割线．（保留作图痕迹，不要求写作法）
    （2）同组的小华思考后提出：能不能设计一种方案，将任意△ABC分割成四个与△ABC相似的小三角形，且其中至少有两个小三角形的相似比不为1？为了研究方便，小华取AB=6，AC=4，BC=5，（如图3）并成功地设计出了分法．请你完成小华的分法，并简单地说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：直线l1与l2相交于点O，对于平面内任意一点M，点M到直线l1、l2的距离分别为p、q，则称有序非负实数对（p，q）是点M的“距离坐标”．根据上述定义，“距离坐标”是（1，2）的点的个数是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p，q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是
    4
    4
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

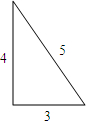    定义：三边长与面积都是整数的三角形称为“整数三角形”．数学学习小组的同学们从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾顺次连接组成三角形，进行探究活动．如图是小亮同学用12根火柴棒，摆成如图所示的“整数三角形”．
    请你分别摆出三个不同的等腰“整数三角形”，画出示意图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：如果一元二次方程ax2+bx+c=0（a≠0）满足a-b+c=0，那么我们称这个方程为“凤凰方程”．已知2x2-mx-n=0是关于x的凤凰方程，m是方程的一个根，则m的值为
    2或-1
    2或-1
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：平面内的两条直线l1与l2相交于点O，对于该平面内任意一点M，M点到直线l1，l2的距离分别为a、b，则称有序非负实数对（a，b）是点M的“距离坐标”．根据上述定义，“距离坐标”为（2，3）的点的个数是（　　）

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年浙江省九年级10月月考数学试卷（解析版） 题型：解答题

    定义：如图，若双曲线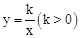与它的其中一条对称轴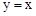相交于两点A，B，则线段AB的长称为双曲线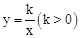的对径．

    （1）求双曲线的对径;

    （2）若某双曲线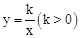对径是.求k的值;

    （3）仿照上述定义,请你定义双曲线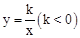的对径.

     

    查看答案和解析>>

    科目：初中数学 来源：2015届北京西城（南区）七年级下学期期末质量检测数学试卷（解析版） 题型：选择题

    定义：平面内的两条直线l与l相交于点O，对于该平面内任意一点M，M点到直线l，l的距离分别为a、b，则称有序非负实数对（a，b）是点M的“距离坐标”．根据上述定义，“距离坐标”为（2，3）的点的个数是

    A. 1         B. 2        C. 3         D. 4

     

    查看答案和解析>>


    同步练习册答案