设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )| A.充分而不必要条件 | B.必要而不充分条件 | | C.充分必要条件 | D.既不充分也不必要条件 |
|
相关习题
科目:高中数学
来源:
题型:
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年天津一中高三(上)第四次月考数学试卷(理)(解析版)
题型:选择题
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学
来源:2012-2013学年新疆巴州尉犁中学高三(上)第二次月考数学试卷(解析版)
题型:选择题
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学
来源:2012-2013学年甘肃省武威五中高三(上)10月月考数学试卷(解析版)
题型:选择题
设φ∈R,则“φ=0”是“f(x)=sin(x+φ)(x∈R)为奇函数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学
来源:2012年安徽省淮北市高考数学二模试卷(文科)(解析版)
题型:填空题
设f(x)=sin(2x+φ),若f(x)≤f(

)对一切x∈R恒成立,则:
①f(-

)=0;
②f(x)的图象关于点(

,0)对称;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+
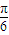
,kπ+

](k∈Z)
以上结论正确的是
(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学
来源:
题型:
设f(x)=x
3(x∈R),若
0≤θ<时,f(m•sinθ)+f(2-m)>0恒成立,则实数m的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:
题型:
(理)设函数f(x)=a
1•sin(x+α
1)+a
2•sin(x+α
2)+…+a
n•sin(x+α
n),其中a
i、α
i(i=1,2,…,n,n∈N
*,n≥2)为已知实常数,x∈R.
下列关于函数f(x)的性质判断正确的命题的序号是
①②③④
①②③④
.
①若
f(0)=f()=0,则f(x)=0对任意实数x恒成立;
②若f(0)=0,则函数f(x)为奇函数;
③若
f()=0,则函数f(x)为偶函数;
④当
f2(0)+f2()≠0时,若f(x
1)=f(x
2)=0,则x
1-x
2=kπ(k∈Z).
查看答案和解析>>

 )对一切x∈R恒成立,则:
)对一切x∈R恒成立,则: )=0;
)=0; ,0)对称;
,0)对称;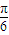 ,kπ+
,kπ+ ](k∈Z)
](k∈Z) )对一切x∈R恒成立,则:
)对一切x∈R恒成立,则: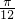 )=0;
)=0;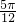 ,0)对称;
,0)对称; ,kπ+
,kπ+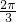 ](k∈Z)
](k∈Z)