
| 已知四边形ABCD和对角线AC、BD,顺次连接各边中点得四边形MNPQ,给出以下6个命题: ①若所得四边形MNPQ为矩形,则原四边形ABCD为菱形; ②若所得四边形MNPQ为菱形,则原四边形ABCD为矩形; ③若所得四边形MNPQ为矩形,则AC⊥BD; ④若所得四边形MNPQ为菱形,则AC=BD; ⑤若所得四边形MNPQ为矩形,则∠BAD=90°; ⑥若所得四边形MNPQ为菱形,则AB=AD.以上命题中,正确的是( )
|
科目:初中数学 来源: 题型:
科目:初中数学 来源:苏州 题型:单选题
| A.①② | B.③④ | C.③④⑤⑥ | D.①②③④ |
科目:初中数学 来源:《第3章 证明(三)》2011年单元测试卷(五)(解析版) 题型:选择题
科目:初中数学 来源:2001年江苏省苏州市中考数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
已知四边形ABCD和对角线AC、BD,顺次连接各边中点得四边形MNPQ,给出以下6个命题:
①若所得四边形MNPQ为矩形,则原四边形ABCD为菱形;
②若所得四边形MNPQ为菱形,则原四边形ABCD为矩形;
③若所得四边形MNPQ为矩形,则AC⊥BD;
④若所得四边形MNPQ为菱形,则AC=BD;
⑤若所得四边形MNPQ为矩形,则∠BAD=90°;
⑥若所得四边形MNPQ为菱形,则AB=AD.
以上命题中,正确的是
科目:初中数学 来源:数学教研室 题型:013
以上命题中,正确的是( )
A.①② B.③④
C.③④⑤⑥ D.①②③④
科目:初中数学 来源:2012年山西省太原市中考数学一模试卷(解析版) 题型:解答题
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
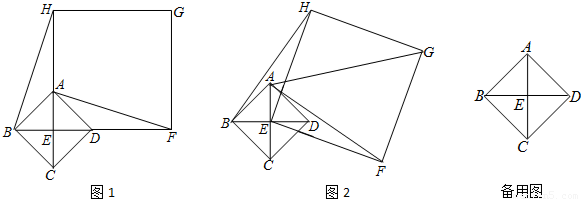
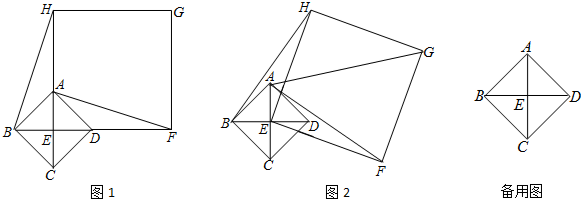
 (2013•顺义区二模)已知:如图,四边形ABCD中,对角线AC、BD相交于点E,∠ABC=∠ACD=90°,AB=BC=6
(2013•顺义区二模)已知:如图,四边形ABCD中,对角线AC、BD相交于点E,∠ABC=∠ACD=90°,AB=BC=6| 2 |
| 2 |
| 3 |
科目:初中数学 来源: 题型:
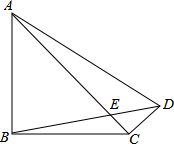
 (2013•顺义区一模)已知:如图,四边形ABCD中,对角线AC、BD相交于点E,BD⊥DC,∠ABD=45°,∠ACD=30°,AD=CD=2
(2013•顺义区一模)已知:如图,四边形ABCD中,对角线AC、BD相交于点E,BD⊥DC,∠ABD=45°,∠ACD=30°,AD=CD=2| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com