相关习题
科目:高中数学
来源:2011-2012学年湖北省武汉外国语学校高二(上)期中数学试卷(理科)(解析版)
题型:选择题
抛物线y=mx
2的焦点坐标为( )
A.

B.
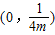
C.
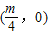
D.
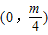
查看答案和解析>>
科目:高中数学
来源:静海县一模
题型:解答题
已知抛物线C:y
2=2px(p>0),其焦点是椭圆mx
2+4y
2=1的右焦点,且椭圆的离心率为
.
(Ⅰ)试求抛物线C的方程;
(Ⅱ)在y轴上截距为2的直线l与抛物线C交于M,N两点,以线段MN为直径的圆过原点,求直线l的方程;
(Ⅲ)若以原点为圆心,以t(t>0)为半径的圆分别交抛物线C上半支和y轴正半轴于A,B两点,直线AB与x轴交于点Q,试用A点的横坐标x
0表示点Q的坐标.
查看答案和解析>>
科目:高中数学
来源:2011年天津市静海县高考数学一模试卷(理科)(解析版)
题型:解答题
已知抛物线C:y
2=2px(p>0),其焦点是椭圆mx
2+4y
2=1的右焦点,且椭圆的离心率为
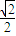
.
(Ⅰ)试求抛物线C的方程;
(Ⅱ)在y轴上截距为2的直线l与抛物线C交于M,N两点,以线段MN为直径的圆过原点,求直线l的方程;
(Ⅲ)若以原点为圆心,以t(t>0)为半径的圆分别交抛物线C上半支和y轴正半轴于A,B两点,直线AB与x轴交于点Q,试用A点的横坐标x
表示点Q的坐标.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2011•静海县一模)已知抛物线C:y
2=2px(p>0),其焦点是椭圆mx
2+4y
2=1的右焦点,且椭圆的离心率为
.
(Ⅰ)试求抛物线C的方程;
(Ⅱ)在y轴上截距为2的直线l与抛物线C交于M,N两点,以线段MN为直径的圆过原点,求直线l的方程;
(Ⅲ)若以原点为圆心,以t(t>0)为半径的圆分别交抛物线C上半支和y轴正半轴于A,B两点,直线AB与x轴交于点Q,试用A点的横坐标x
0表示点Q的坐标.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省名校新高考研究联盟高三(上)12月联考数学试卷(文科)(解析版)
题型:解答题
在直角坐标系xOy中,点

,点F为抛物线C:y=mx
2(m>0)的焦点,线段MF恰被抛物线C平分.
(Ⅰ)求m的值;
(Ⅱ)过点M作直线l交抛物线C于A,B两点,设直线FA、FM、FB的斜率分别为k
1、k
2、k
3,问k
1,k
2,k
3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省绍兴一中高三(下)回头考数学试卷(文科)(解析版)
题型:解答题
在直角坐标系xOy中,点

,点F为抛物线C:y=mx
2(m>0)的焦点,线段MF恰被抛物线C平分.
(Ⅰ)求m的值;
(Ⅱ)过点M作直线l交抛物线C于A,B两点,设直线FA、FM、FB的斜率分别为k
1、k
2、k
3,问k
1,k
2,k
3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省名校新高考研究联盟高三(上)12月联考数学试卷(文科)(解析版)
题型:解答题
在直角坐标系xOy中,点

,点F为抛物线C:y=mx
2(m>0)的焦点,线段MF恰被抛物线C平分.
(Ⅰ)求m的值;
(Ⅱ)过点M作直线l交抛物线C于A,B两点,设直线FA、FM、FB的斜率分别为k
1、k
2、k
3,问k
1,k
2,k
3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
在直角坐标系xOy中,点
M(2,-),点F为抛物线C:y=mx
2(m>0)的焦点,线段MF恰被抛物线C平分.
(Ⅰ)求m的值;
(Ⅱ)过点M作直线l交抛物线C于A,B两点,设直线FA、FM、FB的斜率分别为k
1、k
2、k
3,问k
1,k
2,k
3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>

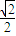 .
. ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分. ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分. ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.